III.2 Retour à l'équilibre d'un matériau excité
Considérons 1 SC isolé, excité de manière homogène.
Les équations de continuité se réduisent à :
et donc
D'où
Remarque :
En régime permanent
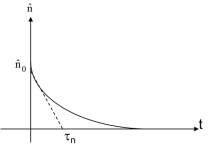
Si on supprime l'excitation à t=0, gn = gp = 0
En intégrant avec, à t=0,
on trouve :
Fondamental :
L'excédent de porteurs décroît exponentiellement avec une constante de temps τ.
Remarque :
Dans le cas d'un matériau dopé en régime de faible inversion, la décroissance des majoritaires est négligeable.