I.3 Relation d'Einstein [La Physique des Semiconducteurs]

I.3 Relation d'Einstein

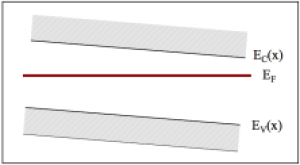
Considérons le semi-conducteur dont la structure de bande est représentée ci contre. Le matériau étant isolé et à l'équilibre thermodynamique, le courant électrique total est nul.

La non homogénéité du matériau entraîne l'apparition d'un champ électrique interne. Deux phénomènes antagonistes vont exister dans la structure.

Un phénomène de diffusion dû à l'inhomogénéité
Un phénomène de conduction dû au champ électrique

Ces deux phénomènes vont s'équilibrer pour donner un courant nul.

Le champ électrique s'écrit : $E (x) = \frac{- dV (x)}{dx} = \frac{1}{q} \frac{{dE}_{C} (x)}{dx}$

En tout point de la structure le courant est nul. Cela se traduit par : $j_{n} (x) = j_{p} (x) = 0$

soit :

$q . n (x) . μ_{n} . E (x) + q . D_{n} \frac{dn}{dx} = 0$

$q . p (x) . μ_{p} . E (x) - q . D_{p} \frac{dp}{dx} = 0$

or $\frac{{dE}_{C} (x)}{dx} = \frac{{dE}_{C} (x)}{dn (x)} . \frac{dn (x)}{dx}$

$n (x) = N . \exp - (\frac{E_{C} (x) - E_{F}}{kT})$

En dérivant n(x) par rapport à Ec on obtient : $\frac{dn (x)}{{dE}_{C} (x)} = \frac{- 1}{kT} . n (x)$

Donc : $E (x) = \frac{1}{q} {dE}_{C} (x) = \frac{- kT}{q} \frac{1}{n (x)} \frac{dn (x)}{dx}$

Or : $E (x) = \frac{- dV (x)}{dx} = \frac{1}{q} \frac{{dE}_{C} (x)}{dx}$

Donc : $(- μ_{n} kT + {qD}_{n}) \frac{dn (x)}{dx} = 0$

Remarque :

On trouve une expression de même type avec les trous.

Pour que ces deux relations soient vérifiées, il faut que :

Définition :

$\frac{D_{n}}{μ_{n}} = \frac{D_{p}}{μ_{p}} = \frac{kT}{q} = U_{T}$ Relation d'Einstein.

Remarque :

La constante de diffusion des porteurs est donc directement liée à leur mobilité.

Fondamental :

Ainsi les courants d'électrons et de trous peuvent indifféremment s'écrire :

$J_{n} = q . D_{n} (n \frac{q}{kT} E + \frac{dn}{dx}) et J_{p} = q . D_{p} (p \frac{q}{kT} E - \frac{dp}{dx})$

$J_{n} = q . μ_{n} (n . E + U_{T} . \frac{dn}{dx}) et J_{p} = q . μ_{p} (p . E - U_{T} . \frac{dp}{dx})$