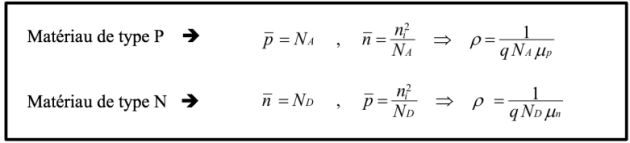I.1 Le courant de conduction

Considérons un gaz d'électrons constitué de N électrons libres. En l'absence de force extérieure appliquée ( Champ électrique), ils se meuvent de façon aléatoire (mouvement brownien).

Rq: la vitesse moyenne est nulle car aucune direction n'est privilégiée.

Entre 2 collisions, le mouvement est rectiligne uniforme, caractérisé par une vitesse appelée vitesse thermique du porteur vth. On obtient cette vitesse en considérant que l'énergie thermique du porteur = son énergie cinétique.

v th = 3 kT m v_{th}= sqrt{ {3kT} over { m} }

Dans le silicium à T = 300K, vth = 107 cm.s-1

l = distance parcourue entre 2 collisions = libre parcours moyen = vth.τc

τc = temps moyen entre 2 collisions.

S nous appliquons une force extérieure, l'équation du mouvement va s'écrire : m d V D ⃗ dt = F ⃗ = q E ⃗ m {d widevec {V} _{D} } over {dt} = widevec {F} =q widevec {E}

Si on l'intègre entre t0 et t0+t, cette équation a pour solution : V D ⃗ = q E ⃗ t m widevec {V} _{D} = q widevec {E}t over {m}

Donc la vitesse augmente linéairement avec le temps entre 2 collisions.

V ⃗ = 1 τ c ∫ 0 τ c V D ⃗ ( t ) dt = q E ⃗ τ c 2 m = q E ⃗ τ R m = μ E ⃗ widevec {V} = {1} over { %tau_{c}} int from{0} to{%tau_{c}} widevec{V} _{D}(t)dt= q widevec {E}%tau_{c} over {2m} = q widevec {E}%tau_{R} over {m}= %mu widevec {E}

τR = temps de relaxation

La vitesse du porteur est donc proportionnelle au champ électrique appliqué.

La constante de proportionnalité est appelée « Mobilité ». Elle est notée par la lettre μ. Elle s'exprime en cm2/V.s

La mobilité représente l'aptitude d'un porteur à se déplacer dans le cristal. Elle est d'autant plus grande que le cristal est pur et que la masse effective du porteur est faible.

Les mobilités des deux types de porteurs diffèrent principalement par la valeur des masses effectives, les électrons étant plus mobiles que les trous. Cela peut se comprendre intuitivement car ils sont à un niveau énergétique supérieur, c'est à dire moins liés à l'atome.

V n ⃗ = μ n E ⃗ et V p ⃗ = μ p E ⃗ widevec {V} _{n} = %mu_{n} widevec {E} ~ ~ ~ ~et ~ ~ ~ ~ widevec {V} _{p} = %mu_{p} widevec {E}

Pour des champs électriques faibles, la loi de proportionnalité est valable. Dès que les champs électriques deviennent importants (quelques kV.cm-1), la vitesse des porteurs devient de l'ordre de grandeur de la vitesse thermique et la mobilité décroît.

Paramètres influant sur la mobilité des porteurs

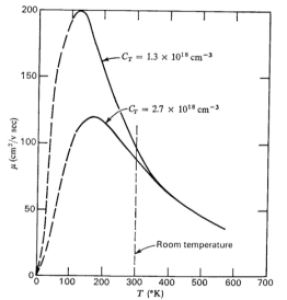
La température :

L'augmentation de température se traduit par une agitation thermique plus importante dans le réseau cristallin et, de ce fait, le temps de relaxation va diminuer car la probabilité de chocs avec les atomes augmente. Il s'en suit une diminution de la mobilité qui suit une loi empirique de la forme :

μ = α . T 3 2 %mu = %alpha .T ^{ {3} wideslash {2} } α est un coefficient qui dépend de la nature du matériau et du type de porteur

Le dopage du matériau :

Les atomes d'impuretés vont influer sur les trajectoires des électrons dans le cristal car, à température ambiante, ils sont tous ionisés. Le nombre de collisions va augmenter et cela va se traduire par une diminution de la mobilité .

Le graphique ci contre montre la variation de m en fonction du dopage dans le cas du silicium.

Mobilité des électrons et des trous dans le Silicium en fonction du dopage à 300KInformationsInformations[1]

Nous venons de montrer que lorsqu'on applique une force extérieure (champ électrique par exemple) à un matériau semi-conducteur, les porteurs vont se déplacer. Il y aura donc apparition d'un courant électrique.

Ce courant de conduction s'écrit : j ⃗ = ρ . V D widevec {j} = %rho .V _{D} dans lequel ρ est la densité de charges ρ = q.N

donc : j ⃗ = q . N . V D = q . N . q τ R m . E ⃗ = σ . E ⃗ widevec {j} =q.N.V _{D}=q.N.{q %tau _{R}} over {m}. widevec {E} = %sigma .widevec {E} avec : σ = q 2 . τ R . N m = q . N . μ %sigma={q ^{2}. %tau _{R}.N} over {m} = q.N. %mu

σ = q . N . μ %sigma= q.N. %mu est appelé conductivité du matériau et s'exprime en Ω-1cm-1.

L'existence de deux types de porteurs va faire apparaître deux courants qui seront additifs (porteurs de charge opposée se déplaçant en sens opposé).

j n ⃗ = σ n . E ⃗ widevec {j} _{n} = %sigma _{n} .widevec {E} et j p ⃗ = σ p . E ⃗ widevec {j} _{p} = %sigma _{p} .widevec {E}

Le courant total de conduction s'écrit donc :

j ⃗ = j n ⃗ + j p ⃗ = ( σ n + σ p ) . E ⃗ widevec {j}=widevec {j} _{n}+widevec {j} _{p} = (%sigma _{n}+%sigma _{p}) .widevec {E}

Définition

La conductivité est donc fonction des densités des deux types de porteurs. Elle s'exprime par la relation suivante.

σ = q ( n ¯ . μ n + p ¯ . μ p ) %sigma = q( bar {n}. %mu _{n}+ bar {p}. %mu _{p})

On a coutume de caractériser les semi-conducteurs par leur résistivité et non par leur conductivité. Elle s'écrit :

ρ = 1 σ = 1 q ( n ¯ . μ n + p ¯ . μ p ) %rho = {1} wideslash { %sigma} = {1} over {q( bar {n}. %mu _{n}+ bar {p}. %mu _{p}) }

Exemple

La résistivité des semiconducteurs intrinsèques usuels est donnée ci-dessous :

Remarque

Les minoritaires étant très peu nombreux devant les majoritaires, leur contribution est négligeable dans le calcul de la résistivité.

On a donc, pour les matériaux dopés :

Fondamental

Dans la réalité, cette condition sera TOUJOURS respectées et la résistivité (ou la conductivité) ne dépendront que de la densité des porteurs Majoritaires.