Application au gaz diatomique
Fonction de partition rotationnelle et vibrationnelle
Rotation :
Pour une molécule diatomique, le moment d'inertie vaut Iα = mR2.
On définit alors θrot la température caractéristique de rotation qui s'écrit alors :
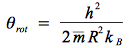
où m est la moyenne barycentrique des masses des deux tomes, R le rayon de rotation (égal à la demi distance de la liaison covalente entre les deux atomes), h et kB les constantes de Planck et de Boltzmann.
Les valeurs typiques pour des molécules sont : 2,86 K pour N2, 85,4 K pour H2, 0.346 K pour Cl2, 15,2 K pour HCl.
On obtient après calcul et approximation à une température supérieure à 5θrot (vérifiée à température ambiante pour Cl2, HCl, N2 mais pas H2 !), pour la fonction de partition rotationnelle :
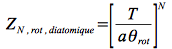
Vibration :
Pour une molécule diatomique et donc linéaire, il n'y a qu'un seul mode de vibration et une température caractéristique de vibration associée θ'vib:
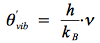
où ν est la fréquence du mode de vibration.
Ex. H2 : θ'vib = 6210 K.
Ex. Cl2 : θ'vib = 810 K.
Ex. N2 : θ'vib = 3340 K.
Ex. HCl : θ'vib = 4140 K.
Ex. CO : θ'vib = 3070 K.
On obtient la fonction de partition vibrationnelle dépendante de la température :
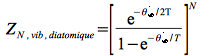
Définition : équation d'état du gaz parfait diatomique
En application de la relation permettant de déduire la pression à partir de la fonction de partition, 
, et sachant que le seul terme dépendant du volume est VN, nous obtenons très facilement :
C'est la même relation que pour un gaz parfait monoatomique, puisque les fonctions de partitions ZN,rot et ZN,vib ne dépendent que de la température et pas du volume.
