Dérivation de la fonction de partition d'un gaz polyatomique
Le problème à résoudre
Ensemble statistique NVT où se trouve un gaz constitué de N molécules polyatomiques toutes identiques dans une boite cubique de volume V = L3 et d'arête L maintenue à température constante T.
les 9N coordonnées 3N positions spatiales,
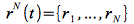où 
+ 3N angles d'Euler anglesNavec i=1,...N + 3N quantité de mouvement, 
Expression de l'Hamiltonien polyatomique
avec :
l'énergie cinétique de translation, sous une forme fonctionnelle très classique 1/2 m.v2
l'énergie cinétique de rotation avec une vitesse de rotation αi et un moment d'inertie Ii
l'énergie cinétique de vibration avec une fréquence de vibration ωij et une amplitude de vibration αij, analogue à une forme d'oscillateur harmonique 1/2 k.x2
l'énergie potentielle VN générale, qui dans le cas d'un potentiel de paire additif s'écrit,
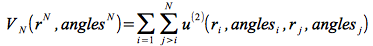
Fonction de partition intégrale polyatomique
Produit de contributions cinétique de translation, de rotation et de vibration et de l'énergie potentielle :
soit
ou encore
QN est appelée intégrale de configuration classique
