Dérivation de la fonction de partition d'un gaz monoatomique
Le problème à résoudre
Nous considérons l'ensemble statistique NVT où se trouve un gaz constitué de N particules monoatomiques toutes identiques dans une boite cubique de volume V = L3 et d'arête L maintenue à température constante T.
les coordonnées permettant de décrire le système sont 3N coordonnées / positions spatiales,
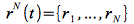 où
où  avec i=1,...N et 3N quantité de mouvement,
avec i=1,...N et 3N quantité de mouvement, 
Etant monoatomiques, l'énergie cinétique des particules comporte uniquement un terme de translation et l'hamiltonien classique s'écrit alors :
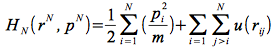 , avec
, avec 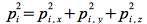
Afin d'illustrer la démarche de façon générale, nous avons conservé un terme d'énergie potentielle non nul, décrit par un potentiel de pair additif u(rij). Pour un gaz parfait, il sera supposé nul., soit aucune interaction.
Fonction de partition intégrale monoatomique classique
En mécanique classique, il est impossible de compter tous les états dégénérés → il faut alors transformer la sommation discrète
 en une intégrale sur les 6N coordonnées :
en une intégrale sur les 6N coordonnées :
ou encore
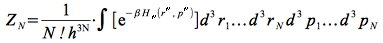
où la notation d3 rappelle qu'il y a une intégrale sur 3 coordonnées cartésiennes pour chaque ri et sur 3 directions de vitesse pour chaque pi.
Le premier dividende N!h3N est un facteur qui garantit la continuité entre mécanique classique et quantique, ZN(quantique)=ZN(N,V,T).
Le terme N! : énumération de tous les états indistinguables.
Le terme h3N rend adimensionnel (sur les 3N coordonnées spatiales) la fonctionnelle continue sous forme d'intégrale. La fonctionnelle discrète issue de la mécanique statistique étant intrinsèquement adimensionnelle. h est la constante de Planck.
Expression de l'Hamiltonien monoatomique
Le Hamiltonien HN,
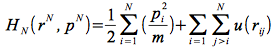 contient un terme d'énergie cinétique de translation :
contient un terme d'énergie cinétique de translation :
et un un potentiel VN quelconque ici exprimé comme un potentiel de paire :
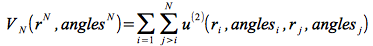 .
.
Intégration du terme cinétique
Ecinétique ne dépend pas des coordonnées x,y,z → nous devons intégrer e-p^2/2m sur dpi.
Or, il existe en mathématique une intégrale définie qui calcule cette intégrale :

Définition : Fonction de partition d'un gaz monoatomique
La fonction de partition d'un gaz monoatomique est exprimée par la relation :

Dans la deuxième expression, nous avons introduit la longueur d'onde de de Broglie.
QN est appelé intégrale de configuration classique et concerne les forces d'interactions existant au sein du système. (Nota Bene, VN peut prendre toutes les formes, notamment celle d'un potentiel de paire additif). (Nota Bene 2 : ne pas confondre V volume et VN potentiel).





