Démonstration alternative de l'équation du viriel : l'approche "cluster"
Nous avons écrit pour un système monoatomique dans l'ensemble canonique NVT, et soumis à un potentiel d'interaction quelconque VN l'expression de la fonction de partition :

De plus, nous considérons un potentiel de paire additif : ![]()
Démonstration
Définissons les fonctions de Mayer qui se rapportent aux interactions deux à deux :
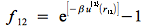
(on peut étendre aux interactions 3 à 3 :
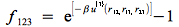 , etc....).
, etc....).La forme particulière de ces fonctions en [exp (-X) -1] fait qu'elles n'ont de valeur significative différente de zéro que lorsque les particules sont proches et donc leur interaction est forte.
L'intégrale de configuration QN s'écrit :

sachant que e(a+b) = ea.eb, on peut écrire l'exponentielle d'une somme comme un produit d'exponentielle :

ensuite, nous détaillons le produit :

dans cette somme la première ligne décrit les interactions entre paires de particules, la deuxième ligne celles entre 3 particules deux à deux, etc...
Les termes de la deuxième ligne ne sont importants que si les deux particules sont proches. Ceux de la troisième ligne ne sont importants que si deux différentes paires de particules sont proches entre elles simultanément. etc...
Par conséquent, en supposant que le nombre total N de particule soit grand et en considérant un gaz dilué (où les particules sont éloignées), nous pouvons conserver seulement les interactions 2 à 2 et écrire l'approximation :

l'intégrale de configuration devient :

Comme auparavant, supposant que les particules sont identiques, la somme contient N(N-1)/2 termes qui contribuent de façon égale dans l'intégrale :
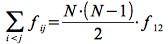
En remplaçant :

où nous avons fait apparaître les intégrants dr3
f12 ne dépendant que de r12, nous pouvons intégrer dr3...drN qui donne VN-2:

En fixant une direction d'intégration à partir d'un point central, nous pouvons transformer l'intégrale volumique sur deux coordonnées en une intégrale radiale :
 nous obtenons :
nous obtenons :
soit :

Nous obtenons l'expression de la fonction de partition :

Prenons maintenant l'expression du potentiel thermodynamique de l'ensemble canonique. C'est la fonction - A/T :
 où A est l'énergie libre :
où A est l'énergie libre :
où nous connaissons Aid la contribution gaz parfait :

Dans l'expression de A nous avons une fonction de la forme ln(1+x) avec x que nous pouvons supposé petit dans notre contexte puisque nous avons supposé plus haut que nous étions dans un gaz dilué.
Nous pouvons donc prendre prendre la série puissance de ln(1+x)= x - x2/2 + x3/3 ... et ne prendre que le premier terme x.
Par ailleurs si N est grand nous pouvons approximer N(N-1) par N2. Nous obtenons :
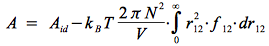
Sachant que
 , nous obtenons :
, nous obtenons :
et finalement l'expression du second coefficient du viriel :
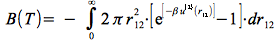
Définition : définition alternative (UTILE) du second coefficient du viriel :
l'expression du second coefficient du viriel est définie par rapport à un potentiel d'interaction de paire additif u(2 par :
![]()
On trouvera dans le chapitre 2 de nombreuses expressions de potentiels de paire : Sphère dure, Puits carré, Lennard Jones, Sutherland, ... qui sont reprisess ci-dessous.





