Energie cinétique moyenne et viriel : le théoème de Clausius
Nous cherchons à calculer l'énergie cinétique moyenne d'un système de particules dans un volume fini. Elles sont supposées sphériques (énergie cinétique de translation uniquement) et interagissent avec un potentiel d'interaction VN.
une force Fi s'exerce sur chaque ième particule. Elle est évaluée à partir du gradient du potentiel
et est composée de contributions provenant des autres particules et des forces extérieures :
La loi de Newton s'écrit :
Et l'énergie cinétique s'écrit :
Démonstration
La démonstration est la suivante :
Nous pouvons écrire l'énergie cinétique de façon alternative comme :
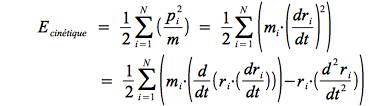
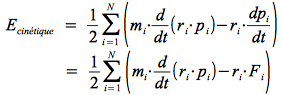
Si nous calculons la moyenne au cours du temps de cette expression (noté avec deux crochets < >t), nous pouvons montrer que le terme d/dt (ri.pi) devient nul sur un intervalle de temps t suffisamment long :
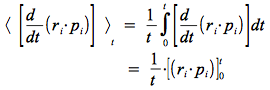
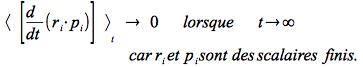
Par ailleurs d'après la définition de la force
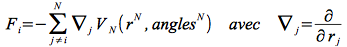, on peut intégrer la force et prendre la moyenne temporelle : L'énergie potentielle moyenne s'écrit alors :
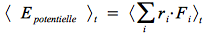
Définition : Théorème du Viriel de Clausius
Nous obtenons l'expression du viriel :
Pour un système système isolé de particules de masse ponctuelles, l'énergie cinétique moyenne est égale l'opposé de la moitié de l'énergie potentielle moyenne.
La troisième expression, le produit de la force et des coordonnées s'appelle le viriel du système Le terme de viriel vient du latin "vis" qui signifie "force".
