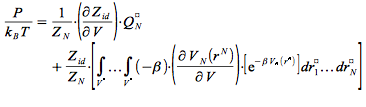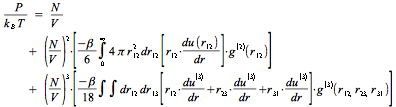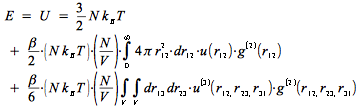Dérivation de l'équation du viriel en pression
Démonstration
Nous avons écrit pour un système monoatomique dans l'ensemble canonique NVT, et soumis à un potentiel d'interaction quelconque VN l'expression de la fonction de partition :
Faisons un changement de variable :
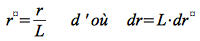et définissons un volume unitaire V ' = V / L3.Nous obtenons :
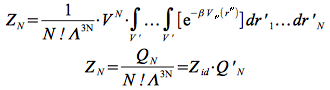
la pression se déduit de la fonction de partition par l'expression habituelle, soit :
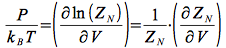
on dérive le produit de fonctions Zid x Q'N :
soit,
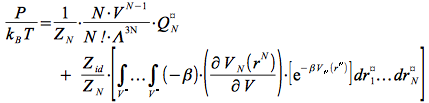
Le premier terme apparaît se simplifie aisément et vaut : N / V ; c'est à dire la contribution du gaz parfait à la pression.
Pour évaluer le deuxième terme, choisissons un potentiel de paire additif, ici exprimé en fonction de la distance entre deux particules r12=|r1 - r2| :
Nous avons donc :
Nous calculons la dérivée partielle du potentiel additif par rapport au volume en exprimant les différentielles :
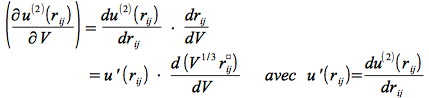
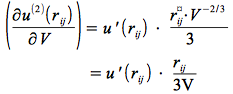
et donc :
Sachant que nous avons supposé que les particules sont identiques, la double somme contient N(N-1)/2 termes qui contribuent de façon égale dans l'intégrale :
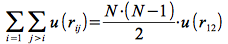
Nous obtenons donc :
Soit en substituant le rapport Zid / ZN par VN / QN :
Remarque : apparition du terme du viriel
en restaurant on élimine le facteur VN=L3N et on remplace r¤ par r. On obtient
REMARQUE : On retrouve dans cette expression le produit "r x u'(r)", c'est à dire un VIRIEL, comme dans le théorème de Clausius
Second coefficient du viriel : première définition
Nous allons faire apparaître dans l'expression précédente la fonction de densité à deux corps ρ(2)(r1,r2):
d'où :
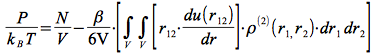
mais également, par définition de la fonction de distribution radiale :
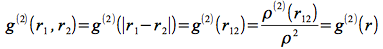
nous écrivons :
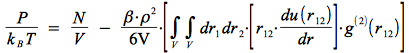
Or en fixant une direction d'intégration à partir d'un point central, nous pouvons transformer l'intégrale volumique sur deux coordonnées en une intégrale radiale :
et nous obtenons l'équation du viriel en pression.
Définition : équation du viriel au second ordre
L'équation du viriel en pression (tronquée au second coefficient) s'écrit :
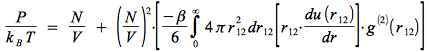
soit
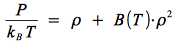
avec B(T) appelé le second coefficient du viriel
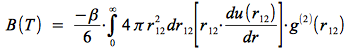
Extension aux forces entre trois corps
Si on tiens compte des forces entre trois corps dans l'expression du potentiel d'interaction VN(rN),
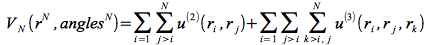on peut démontrer de façon analogue qu'il faut introduire une correction dépendant de u(3) et de la fonction de corrélation à 3 corps g(3) : 
et introduire C(T), le troisième coefficient du viriel:
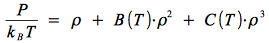
avec
Expression de l'énergie interne
de la même manière, on peut obtenir l'expression de l'énergie faisant intervenir les fonctions de corrélation à 2 corps, g(2) et 3 corps g(3) :
Remarque : hypothèses et avantages
Hypothèses
Dans la démonstration au-dessus, on a fait l'hypothèse d'un fluide isotrope et homogène. Lever cette hypothèse conduit à des expressions analogues mais complique significativement les démonstrations. Cf. l'ouvrage de Lee, 1988[1].
Avantages
Les expressions de la pression et de l'énergie interne obtenues ont permis de réduire le problème de départ, implication l'interaction entre toutes les particules à une somme de contributions indépendantes liées de façon aux interactions 2 à 2, 3 à 3 ...
Par ailleurs la fonction de distribution radiale peut être évaluée par de nombreux modèles et mesurées par plusieurs techniques. Ce n'est pas le cas de la fonction de partition ZN avec laquelle nous étions resté dans les chapitres 3 pour déterminer les grandeurs thermodynamiques et chapitre 4 pour établir quelques équations d'état simple, notamment celle des gaz parfaits.
