Nombres complexes et analyse de Fourier

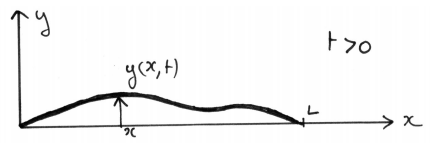
On étudie l'équation d'une corde tendue flexible. Initialement la corde est tendue le long de l'axe des x entre x=0 et x=L (voir figure 3-2.11), puis elle est mise en mouvement (Figure 3-2.12). La fonction y(x,t) représente le déplacement vertical d'un point de la corde.

Pour de petites vibrations de la corde autour de sa position initiale, les lois de la mécanique aboutissent à l'équations aux dérivées partielles suivante :

Comme la corde reste fixée à ses deux extrémités, on aura :

La forme de la corde à l'instant initial est donnée par :

, avec f fonction quelconque.

Enfin, la corde est lâchée sans vitesse initiale donc :

Comme dans le problème précédent, on utilise la méthode de séparation des variables et on pose : puis on remplace dans l'équation 3-2.7.

Comme dans le cas de la barre chaufée, on aura alors :

Les variables x et t sont indépendantes et l'égalité de l'équation ci-dessus n'a lieu que si la valeur commune du rapport est une constante que l'on note 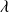. On en déduit deux équations différentielles :

Le signe de 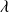impose la forme des familles de solution. Si 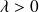, alors la solution de l'équation 3-2.10 est de la forme :

Les conditions aux limites imposent que le déplacement de la corde soit toujours nul en et en ce qui conduit alors à 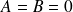, donc à et . La solution nulle n'est pas la solution du problème car à 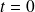, on a 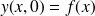. On en déduit que 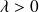et pour simplifier les notation on pose .

La solution de 3-2.10 est de la forme :

Les conditions aux limites imposent que le déplacement de la corde soit toujours nul en et en ce qui conduit alors à , puis à . Il existe un entier n tel que .

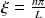D'où la famille des solutions possibles pour la fonction X :

On continue avec la résolution de l'évolution temporelle 3-2.11 :

Et donc :

La corde est lâchée sans vitesse initiale donc :

Ceci conduit à :

D'où et :

Il nous reste à satisfaire la condition initiale 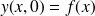ce qui s'écrit :

D'après la théorie des séries de Fourier, les coefficients 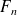sont les coefficients de Fourier de la fonction 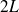-périodique impaire et égale à 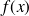sur .

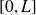On aura donc :

La solution complète du problème posé est alors :

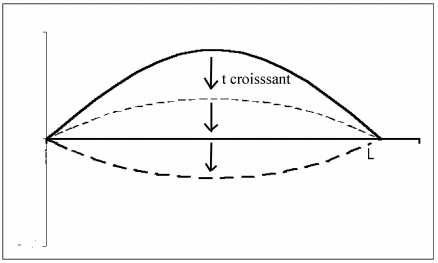
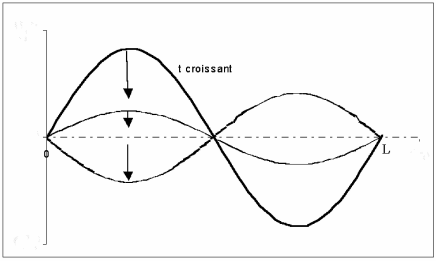
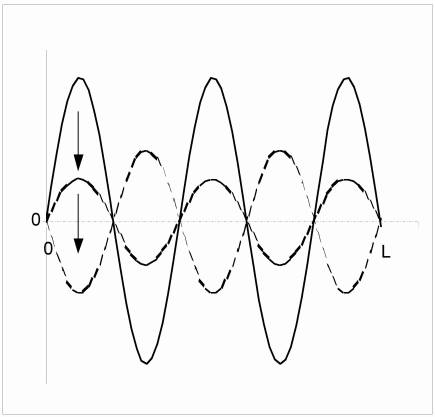
Les termes de cette série représentent les modes naturelles de vibration. La fréquence la plus basse ou fréquence fondamentale est donnée par 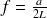, les autres fréquences en sont les multiples (harmoniques). Le schéma ci-dessus montre l'évolution dans le temps et l'espace du premier terme de la série. Le schéma suivant celle deuxième et le dernier celle du cinquième.