Equation de propagation de la chaleur
Comme nous venons de le voir, il s'agit d'un exemple historique car c'est pour le résoudre que Joseph Fourier a formalisé l'utilisation des séries trigonométriques.
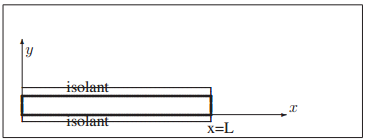
On considère une barre rectiligne de composition et de propriétés homogènes dont l'axe coïncide avec l'axe Ox et dont la température T est une fonction du temps t et de la position dans l'espace x qui représente l'abscisse d'un point de la barre. On considère la section de la barre petite devant sa longueur et les pertes de chaleur par les cotés de la barre négligeables de telle sorte que la température
soit uniforme dans une section située à l'abscisse x.
L'équation de propagation de la chaleur dans la barre s'écrit alors :
On peut relier
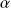à la conductivité thermique du matériau
, à sa chaleur spécifique
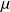et à sa densité (masse par unité de volume)
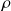par la relation
.
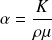La donnée de la température dans la barre à un instant initial (conditions initiales) et de la température aux extrémités de la barre (ou du flux de chaleur) pour les instants ultérieurs suffit à préciser le problème et permet d'en calculer l'unique solution dans le cas ou K,
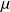et
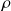ne dépendent pas (en réalité très peu) de la température. On va d'abord déterminer les solutions
de l'équation 3-1.1 qui peuvent se mettre sous la forme
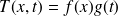c'est-à-dire qui sont à variables séparables (temps et abscisse interviennent séparément). Cette technique est très courante. On remplace dans l'équation 3-1.1 et
on a :
Si on suppose que les fonctions f et g ne sont pas partout nulles, on divise par
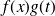et on peut écrire cette équation :
Car les variables x et t sont indépendantes et l'égalité de l'équation ci-dessus n'a lieu que si la valeur commune du rapport est une constante que l'on note
.
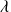On en déduit deux équations différentielles :
L'équation différentielle 3-1.6 a comme solution
avec A constante réelle.
L'équation 3-1.5 doit être résolue en distinguant trois cas, selon le signe de
.
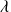On pose
et on aura
avec C et D constantes réelles ;
Alors,
avec C et D constantes réelles ;
On pose
et on aura
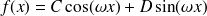avec C et D constantes réelles ;
Ce sont les conditions aux limites et les conditions initiales du problème qui vont nous permettre de finir de déterminer la solution.
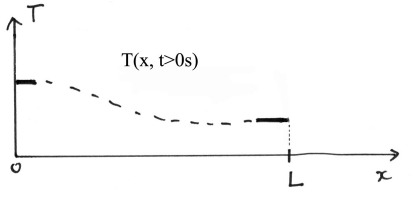
On suppose que le profil de température dans la barre ne varie pas aux extrémités (cf. Figure3-1.8) et est tel que :
et
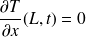
Ces conditions vont nous permettre, dans les trois cas, de déterminer les constantes d'intégration A, C et D.
donc en dérivant par rapport à x et en se plaçant en
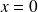on aura pour tout t :
soit
. En se plaçant en
:
, soit
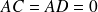et
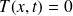, solution exclue ;
donc
et
. Il faut
car
donne la solution nulle exclue. On arrive donc à
constante qui est une solution possible ;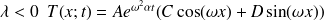
, on procède de même et
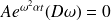pout tout t conduit à
. Ensuite, en
,
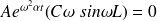soit
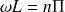avec n entier. Notons que le cas particulier
revient à la solution constante développée pour
;
On obtient donc une famille de solutions particulières de la forme :
Mais où sont donc les séries de Fourier ? En fait elles interviennent dans le calcul final des coefficients
grâce à la donnée de la température initiale de la barre qui va nous permettre de finir de résoudre le problème.
Supposons que le température à
soit donnée en degré Celsius dans la barre par (cf. Figure 3-1.9) :
On doit alors avoir pour t=0 :
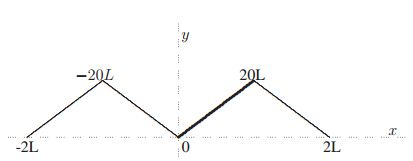
Les coefficients
sont donc les coefficients de Fourier de la fonction 2L-périodique paire et égale à
sur
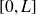. La fonction étudiée est rendue périodique et est décrite dans le graphe ci dessous.
Il suffit, en utilisant les définitions de la semaine 2 de calculer les coefficients de Fourier de cette fonction paire et on arrive à :
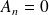si n est pair et peut s'écrire
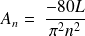si n est impair et peut s'écrire
Donc,
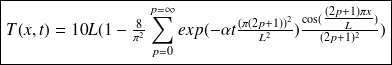
Le premier exercice de la série 1 (ex 7.1) consiste à reprendre le même problème avec d'autres conditions aux limites.
