Backward stability of relaxed GMRES
Assumptions on
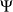and
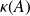
We assume that
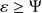and that
and
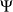are small enough compared to $\kappa(A)$ in such a way that
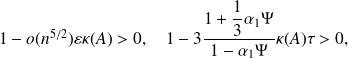
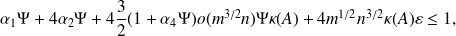
and
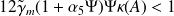
hold, where
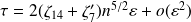, and where the
,
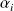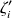and
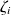are positive constants.
Assumptions on the matrix-vector product
We assume that at each step the error
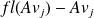made on the quantity
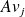is such that
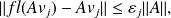where
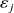is controlled via
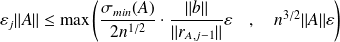
and
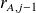is the Arnoldi residual of the relaxed GMRES algorithm.
At step
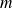of the relaxed GMRES, we define the approximate solution
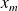by
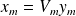, this matrix-vector product being performed exactly on the computed quantities
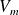and
.
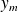Backward error at the "breakdown"
We assume
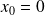and that the algorithm is run until one of the two following conditions holds,
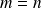,or
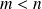and
.
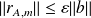Then the residual
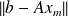satisfies
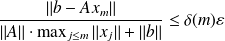
where $\delta$ is a polynomial that depends on the size of the problem and the characteristics of the floating-point arithmetic.
Conclusion
Relaxation for GMRES understood in exact arithmetic.
Relaxation for Householder GMRES in finite precision proved.
Numerous applications for these ideas (FMM, inexact preconditioning).
