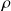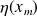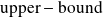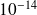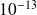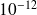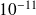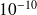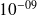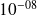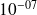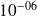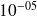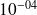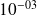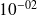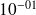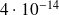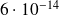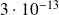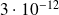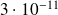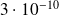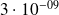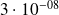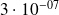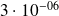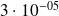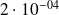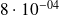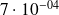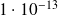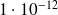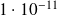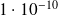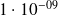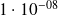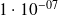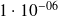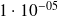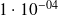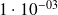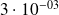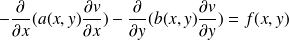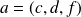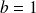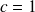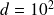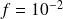Applications
Application I : Variable preconditioning
Inexact left preconditioning in GMRES (II)
Left preconditioning : solve
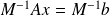 .
.GMRES, inexact left preconditioning :
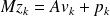 .
.Inexact Arnoldi relation reads
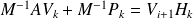 , with
, with
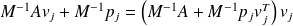
Set
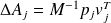 , then
, then
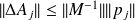 .
.
Inexact left preconditioning(II)
Inexact left preconditioning
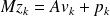 in GMRES}
in GMRES}
Application of theorem for relaxed GMRES
Let
 , such that
, such that
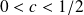 and consider the use of the strategy that generates perturbations in the preconditioning step by introducing residuals which norm are monitored by
and consider the use of the strategy that generates perturbations in the preconditioning step by introducing residuals which norm are monitored by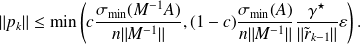
The corresponding relaxed left preconditioned GMRES algorithm is such that at the breakdown of the method, the norm of the preconditioned backward error is less than
 .
.
Inexact right preconditioning in GMRES (I)
Right preconditioning : solve
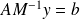 , then
, then
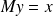 .
.GMRES, inexact right preconditioning :
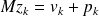 .
.Inexact Arnoldi relation reads
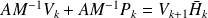 , with
, with
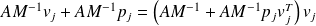
Set
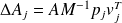 , then
, then
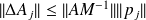 .
.
Inexact right preconditioning (II)
Inexact right preconditioning
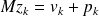 in GMRES
in GMRES
Let
 , such that
, such that
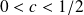 and consider the use of the strategy that generates perturbations in the preconditioning step by introducing residual which norm is monitored by
and consider the use of the strategy that generates perturbations in the preconditioning step by introducing residual which norm is monitored by
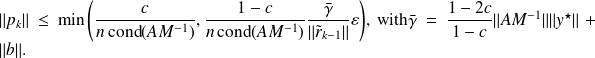 .
.
The corresponding relaxed right preconditioned GMRES algorithm is such that at the breakdown of the method, the norm of the backward error of
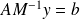 computed at the preconditioned variable
computed at the preconditioned variable
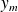 is less than
is less than
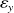 .
.
Obtaining the solution x from y_m
To get the solution to the original system
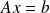 an additional preconditioning operation
an additional preconditioning operation
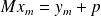 has to be performed, and let
has to be performed, and let
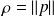 . Suppose that the relaxed right-preconditioned GMRES is run on
. Suppose that the relaxed right-preconditioned GMRES is run on
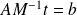 using the strategy of the previous theorem and that
using the strategy of the previous theorem and that
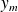 is the corresponding estimate of
is the corresponding estimate of
 . Suppose in addition that
. Suppose in addition that
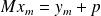 , with
, with
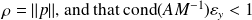 .
.
The backward error
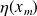 of
of
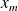 considered as a solution of
considered as a solution of
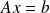 satisfies
satisfies
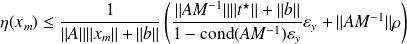 ,
,
where
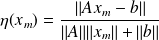 .
.
Tightness of the bound on an example
GMRES with relaxed right preconditioner
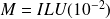 , Matrix
, Matrix
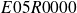 ,
,
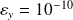 .
.
|
|
|
|
|
|
Application II : Variable FMM in Electromagnetics (BEM)
Relaxed FMM in the solution of 3D Maxwell Equations (Langou (2003))
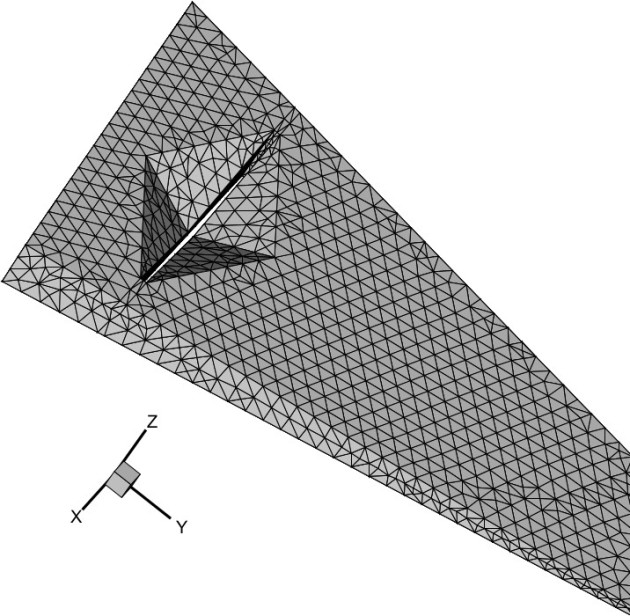
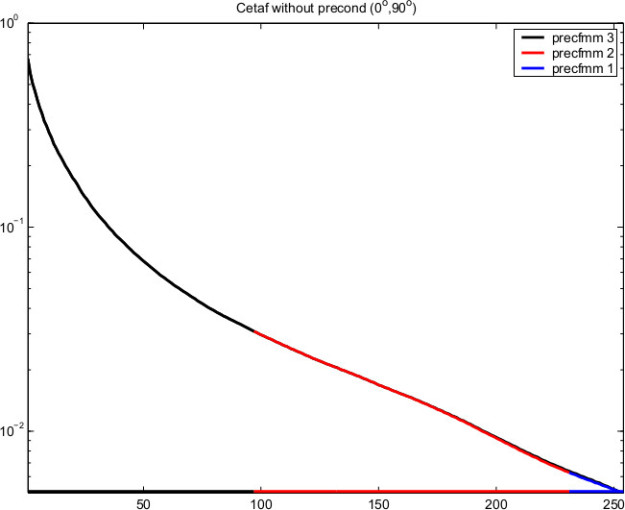
Aplication III : Domain decomposition
Non-overlapping domain decomposition (BFG 00)
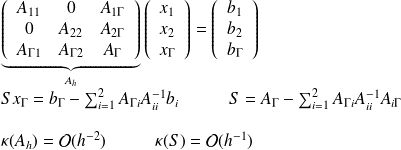
Inner-outer iterations in domain decomposition methods
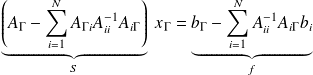
Outer scheme : solve
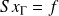 with the Conjugate Gradient (CG).
with the Conjugate Gradient (CG).
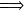 each matrix-vector product
each matrix-vector product
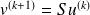 involves
involves
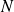 local linear systems
local linear systems
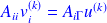
solved in turn by CG:
Inner-outer dependency
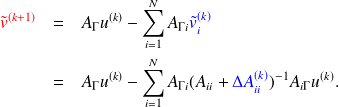
Up to the first order:
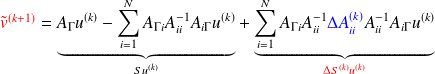
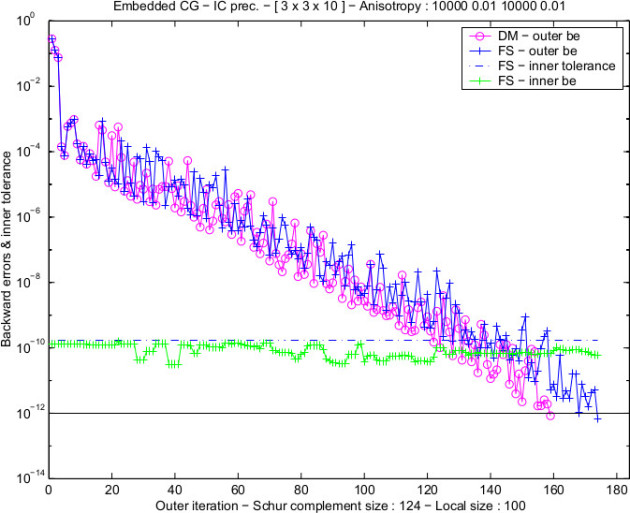
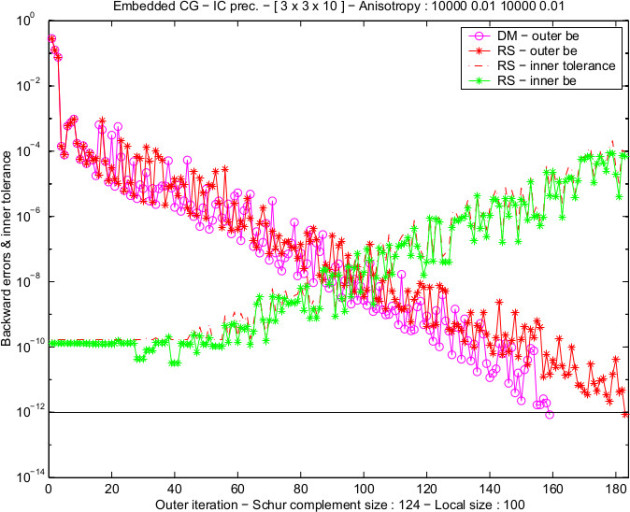
Numerical experiments: a typical case
Anis -
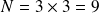 subdomains
subdomainsEach subdomain :
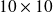 grid points
grid points :
:
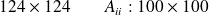
Inner preconditioner : Incomplete Cholesky (IC)
Targeted accuracy:
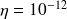
Comparison with a
Experiments using MATLAB