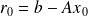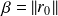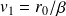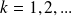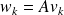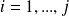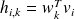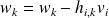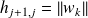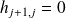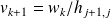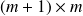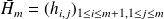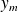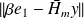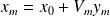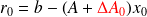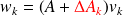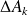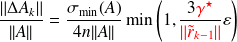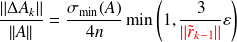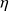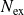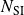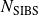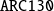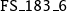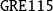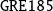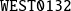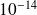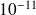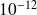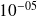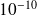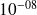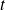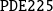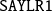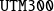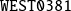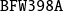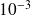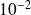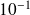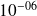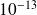Convergence of relaxed GMRES in exact arithmetic
GMRES for solving Ax = b
The Arnoldi algorithm
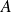 an
an
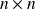 non singular matrix.
non singular matrix.Krylov subspace
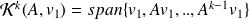
Arnoldi algorithm on
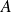 , startineg with
, startineg with
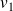 generates an orthonormal set of vectors
generates an orthonormal set of vectors
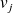 such that
such that
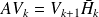 , with
, with
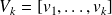 ,
,
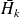 upper-Hessenberg.
upper-Hessenberg.Breakdown of the algorithm when
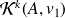 is an
is an
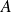 -invariant subspace.
-invariant subspace.
Krylov solvers for Ax=b(Van der Vorst(03))
Iterate in the Krylov space
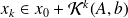
The Ritz-Galerkin approach (e.g. FOM, Lanczos method, CG) :
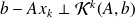
The minimum norm residual approach (e.g. GMRES, MINRES) :

The Petrov-Galerkin approach (e.g. BiCG, QMR)
The minimum norm error approach (e.g. SYMMLQ) :

The GMRES method
The GMRES iterate is the vector of
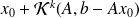 such that
such that
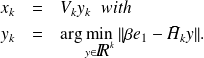
The minimizer
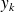 is n general inexpeensive to compute since it requires the solution of an
is n general inexpeensive to compute since it requires the solution of an
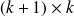 linear least-squares problem.
linear least-squares problem.
|
The inexact GMRES for solving Ax = b
Inexact GMRES method
Take the basic GMRES method,
And perturb the matrix-vector products
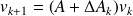 . Easy way to control the inner accuracy.
. Easy way to control the inner accuracy.Why ?
The matrix is not known with full accuracy (Parameter estimation, Schur complement,...)
Computing
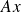 with a poor accuracy is cheap (FMM)
with a poor accuracy is cheap (FMM)
|
Consider the normwise backward error
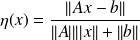 , and
, and
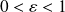 .
.
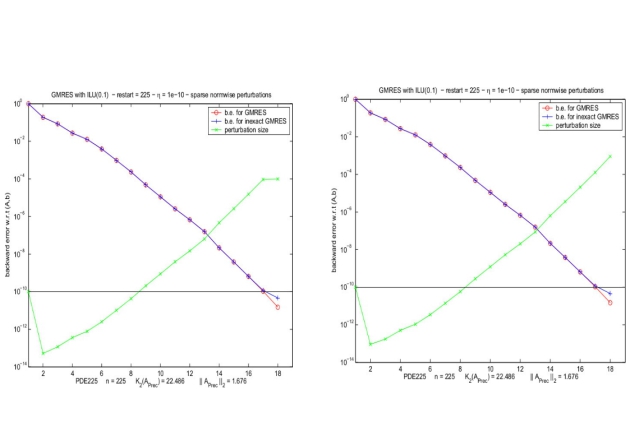
Abundant numerical illustration in Bouras, Frayssé, Giraud (00) and Bouras, Frayssé (04) reports that if a {\color{red}{relaxed}} GMRES is run on a computer,
using perturbations controlled so that
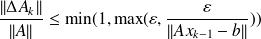 ,
, The GMRES iterate
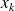 reaches for some
reaches for some
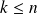 a backward error
a backward error
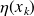 less than
less than
 .
.
Some properties of the BFG criterion
BFG criterion
 ,
,Never perform perturbations
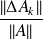
smaller than the target backward error
 ,
,greater than

Theoretical criterion : knowledge of the exact
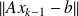 required.
required.Scaling issues ...
Scaling issue
Let
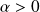 . Arnoldi relation
. Arnoldi relation
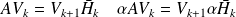
Invariance of the backward error of the
 GMRES iterates, while considering
GMRES iterates, while considering 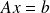 , initial guess
, initial guess
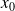
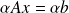 , initial guess
, initial guess
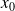
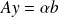 , initial guess
, initial guess
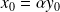
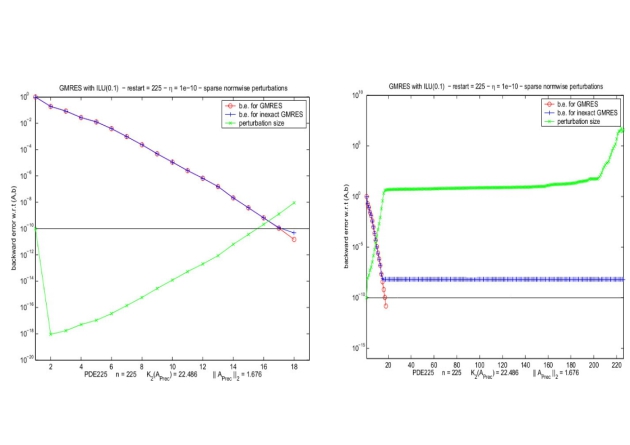
In practice, if the control is not scaling invariant, the perturbation size allowed by the relaxation criterion might be arbitrarily small/large.
This might prevent the relaxed algorithm from converging to
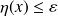 .
.
Convergence analysis in exact arithmetic
Exact relations in the inexact algorithm
Exact arithmetic assumed
From the Gram-Schmidt process follows the inexact Arnoldi relation
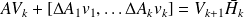
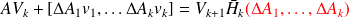
Least squares
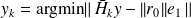
True residual
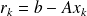
Computed residual
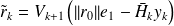 . The norm
. The norm
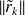 is readily available from the incremental solution of the least squares
is readily available from the incremental solution of the least squares
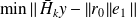
Inexact GMRES algorithm as an exact GMRES on a perturbed matrix
Van den Eshof, Slejpen (04) and Szyld, Simoncini (03) define
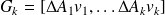 . The inexact Arnoldi reads
. The inexact Arnoldi reads
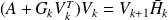 .
.
The computed residuals norm
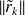 are non increasing,
are non increasing,there exists a family of matrices
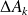 such that {
such that {
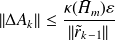
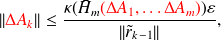 ,
,
 , then
, then
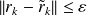
Information on the exact residual obtained from
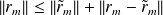
View
 GMRES as a
GMRES as a
 GMRES :
GMRES :
The inexact Arnoldi relation reads

The breakdown of Flexible GMRES studied in (Saad (03)) shows that an happy breakdown at step
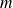 (
(
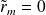 ) occurs if
) occurs if
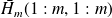 is nonsingular.
is nonsingular..The happy breakdown
In the case of Flexible GMRES, the solution to the original system is
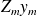 .
.In the inexact method,
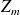 is not available.
is not available.
Forthcoming activity : derive a relaxation strategy such that an happy breakdown necessarily occurs and that
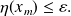
Sufficient convergence condition for the relaxed GMRES
Let
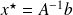 . If
. If
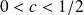 , and if the perturbations are such that,
, and if the perturbations are such that,
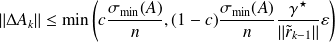 b where \
b where \
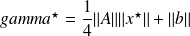 then at the breakdown,
then at the breakdown,
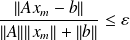 .
.
Requires only the computed residual.
Approximations of
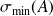 and
and
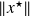 needed.
needed.Replacing
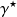 by
by
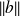 leads to a more stringent criterion in which
leads to a more stringent criterion in which
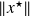 is not needed.
is not needed.
Numerical illustration on academic examples
Description of the experiments
Backward stability of Householder GMRES
Result of J.~Drkosova and M.Rozloznik and Z.Strakos and A.~Greenbaum(95) shows that if
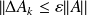 , the Householder GMRES running using the working precision
, the Householder GMRES running using the working precision
 reaches a backward error
reaches a backward error
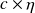 , where
, where
 depends on the problem size and on the details of the arithmetic.
depends on the problem size and on the details of the arithmetic.Empirical Strategy SIBS defined by
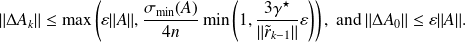
In this case, perturbations are never smaller than
 .
.
Inexact products | |||||
matrix |
|
|
|
|
|
-
-
-
-
| 130 130 183 183 115 115 185 185 132 132 |
| 15 12 40 45 79 52 161 157 130 116 | 15 12 40 47 79 53 161 157 130 108 | 15 12 43 48 79 53 161 157 130 108 |
Inexact products | |||||||
matrix |
|
|
|
|
|
|
|
- -
- -
-
-
-
-
| 236 236 236 236 115 185 185 185 343 317 225 225 238 238 300 300 381 381 398 398 |
| 10 20 20 20 10 10 10 15 10 10 10 10 10 10 15 15 10 10 20 20 |
| 26 79 57 34 17 81 50 27 38 21 26 24 199 147 45 30 21 15 144 88 | 27 80 58 36 17 84 60 28 39 21 26 25 198 148 46 30 21 18 156 96 | 27 80 58 37 17 84 60 28 39 21 26 25 198 148 746 30 21 18 156 96 |