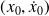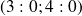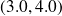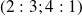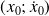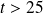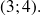Estimation under the linearity assumption.
Best Linear Unbiased Estimation (BLUE)
Consider the linear model
 where
where
 is deterministic and
is deterministic and
 is a random vector satisfying
is a random vector satisfying
Definition :
The
 estimator for
estimator for
 from
from
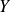 is the random vector
is the random vector
 which minimizes
which minimizes
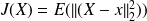 subject to
subject to
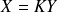 and
and
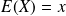
Fundamental : Theorem
If
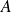 has full rank, the BLUE is
has full rank, the BLUE is
Proof
Starting from
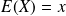 we get
we get
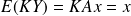 . This equality should hold for any x, i.e.
. This equality should hold for any x, i.e.
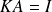 . We have
. We have
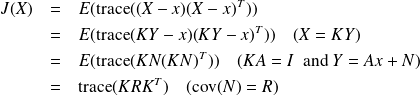
Set
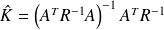 , and write
, and write
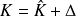 . From
. From
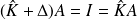 , we get
, we get
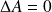
Furthermore,
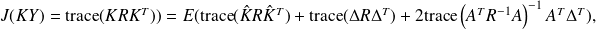 and
and
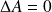 yields
yields
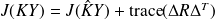 .
.
Since
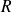 is positive definite,
is positive definite,
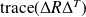 is a scalar product for
is a scalar product for
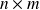 matrices, and
matrices, and
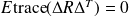 , if and only if
, if and only if
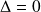
Optimal Least mean squares estimation I
We consider the random vector
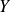 defined by
defined by
 where
where
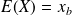 ,
,
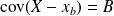
and
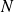 is such that
is such that
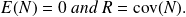
Let us also assume that
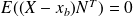 (uncorrelated pair). For a random vector
(uncorrelated pair). For a random vector
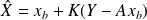 ,
,
we define the error covariance matrix
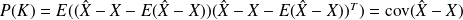
Definition :
The optimal least mean squares estimator
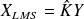 is such that
is such that
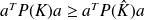 for every matrix
for every matrix
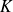 and every vector
and every vector
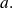 This variational property is written in short
This variational property is written in short
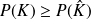
Optimal Least mean squares estimation II
Fundamental : Theorem
The Optimal Least mean squares is obtained for
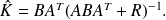
The associated covariance matrix is
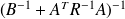 .
.
Proof
We set
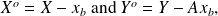 then
then
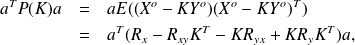
where
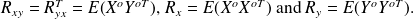
Differentiating this expression with respect to
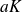 and setting the derivative to
and setting the derivative to
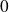 gives to
gives to
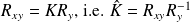
A direct computation shows that
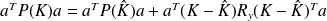 , which shows that
, which shows that
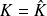 is the unique solution.
is the unique solution.
In addition,
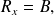
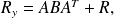 and
and
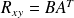 , which shows that
, which shows that
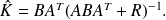
Then
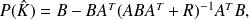 and the result follows from the Sherman-Morrison formula.
and the result follows from the Sherman-Morrison formula.
Conclusion
Assume that the random vector
 defined by
defined by
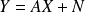 , where
, where
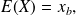
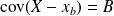 and
and
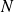 is such that
is such that
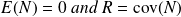
Under various statistical approaches, if the realization
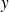 of
of
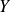 is available, it is reasonable to estimate
is available, it is reasonable to estimate
 as the minimizer of the quadratic functional
as the minimizer of the quadratic functional
The solution of the problem is unique and can be expressed as
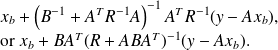
Conclusion : the 4D Var functional
We assume that at
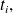
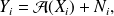
where
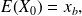
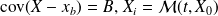 and
and
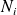 is such that
is such that
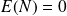 and
and
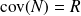
We are looking for an estimation of
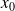 that minimizes
that minimizes
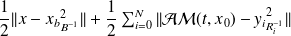
The above functional is called the
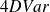 functional.
functional.
A Data Assimilation experiment I
We consider the problem of estimating inital conditions
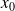 and
and
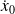 of the system described by
of the system described by
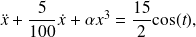 from (possibly noisy) observations of
from (possibly noisy) observations of
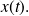
The parameter
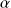 controls the nonlinearity of the problem. For
controls the nonlinearity of the problem. For
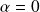 , if
, if
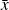 is a particular solution of the problem for zero initial conditions, all the solutions are expressed by
is a particular solution of the problem for zero initial conditions, all the solutions are expressed by

Assume that noisy observations
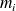 of
of
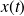 are available at
are available at
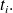
We want to minimize the linear least-squares functional
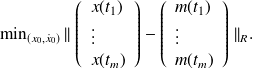
A Data Assimilation experiment II
Solving the linear least squares problem (
 )
)
For each observed quantity
 , computation of the linear theoretical counterpart
, computation of the linear theoretical counterpart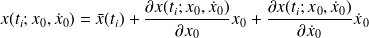
Solution of the linear least-squares problem, using either a direct method (for problem sizes that are small compared to the computer characteristics) or use e.g. a Conjugate Gradient based iterative solver.
We take
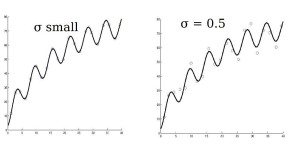
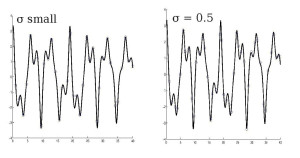
Linear case : exact observations (zero noise) v.s. noisy obs.
Linear case : exact observations (zero noise) v.s. noisy obs.
A Data Assimilation experiment III
Solving the linear least squares problem (
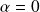 )
)
Solution based on linearizations of the dynamics around
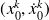 Starting point
Starting point
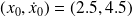
For each observed quantity
 , computation of the linear theoretical counterpart is
, computation of the linear theoretical counterpart is 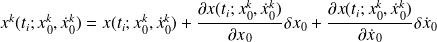
Update
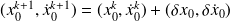
Solution of the linear least-squares problem, using either a direct method (for problem sizes that are small
compared to the computer characteristics) or use e.g. a Conjugate Gradient based iterative solver.
We take
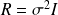 .
.
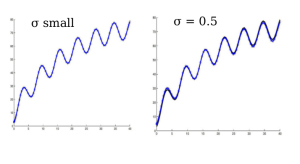
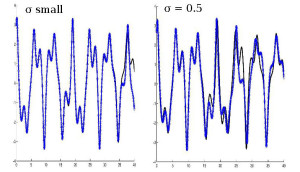
Non Linear case : exact observations (zero noise) v.s. noisy obs.
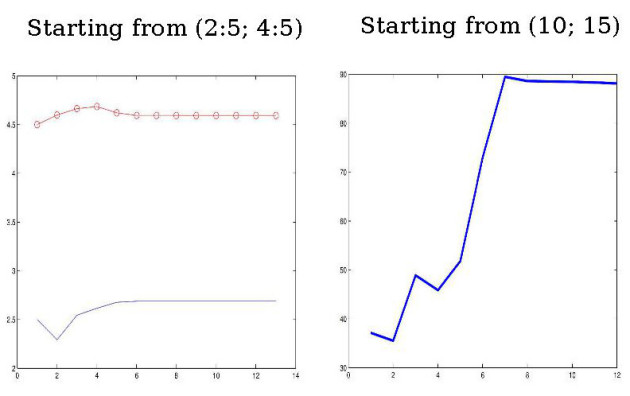
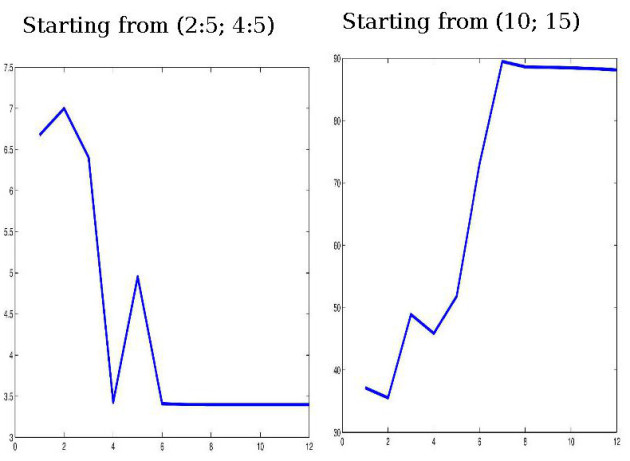
Coping with nonlinearity : guess for the analysis
The Gauss-Newton algorithm for
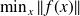 reads :
reads : Choose
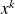 , solve
, solve
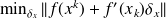 , update
, update
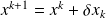 .
.A critical point of
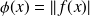 | is a point where
| is a point where
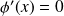 .
.In the case of nonlinear least-squares problems, the Gauss-Newton algorithm does not converge from any stating point to a critical point.In the case of nonlinear least-squares problems, the Gauss-Newton algorithm does not converge from any stating point to a critical point.