Estimation under the Gaussian assumption
Definition :
Suppose a random vector
has a joint probability function
, where
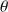is an unknown parameter vector.
Suppose
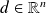is a realization of
A maximum likelihood estimator for
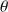given d is a parameter that maximizes the log likelihood function
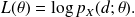
Example :
Suppose
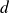is a realization of a Gaussian vector
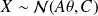, where the parameter
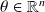is unknown. The log likelihood is
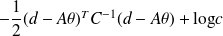, and
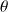is the solution of the linear least-squares problem
.
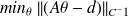Some rationale for the maximum likelihood
The information we have is that
is a realization of
. We have (make a picture involving disjoint sets)
Therefore if
is enlarged, the probability that
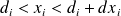(i.e. d is close to a realization of
) is increased). Note that
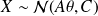, is equivalent to
.
Inclusion of a priori information on thêta
We may want to incorporate additonal information by viewing the parameter vector
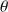as a realization of a random vector
.This analysis is refered to as Bayesian estimation
It relies on the notion of conditional probability given
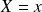, defined by the function of
:
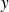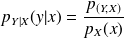
If
and
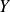are independant random vectors
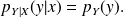
Definition :
The maximum a posteriori estimator maximizes
over
. Is is a function of
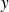
Example :
We consider the random vector Y defined by
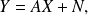where
and
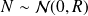are two independent random vectors.
Let
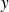be a realization of
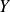. The MAP of
is
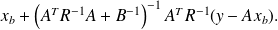
Proof
The Bayes'law reads
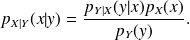
Since
,
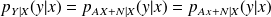from the independence of
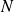and
we get
.
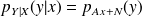From
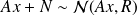we get
.
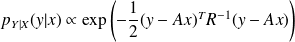In addition,
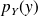does not depend on
and
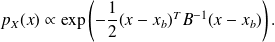
Therefore, the MAP minimizes
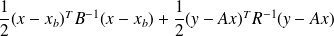
The random vectors are assumed Gaussian. However there might be systematic errors making the estimation unreliable.
Suppose
and
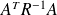is nonsingular. Then
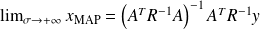, and we recover the maximum likelihood estimator.The useful matrix equality (Sherman-Morrison)
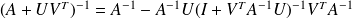can be used to show that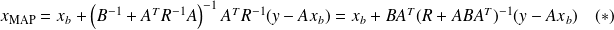
These two formula are computationally very different when
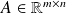is such that
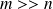or
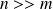.The maximum likelihood estimation works for nonlinear A and leads to
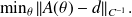
Proof of (*)
From the SM formula, we get
which yields
.
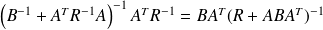