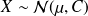Preliminary definitions and notations
Definition :
A probability space is the triplet
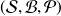where :
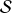is the sample space,
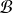is a collection of subsets of
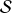
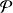is a probability function (i.e.
,
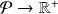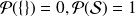and for countable disjoints sets,
)
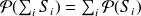Definition :
A random variable is a measurable function
.
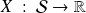Definition :
The cumulative distribution of
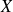is the function
.
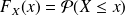Definition :
The mean or expectation of a random variable
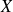is defined by
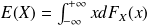
for a continuous vartiable (our case),
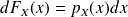. The expectation operator is linear.
Definition :
Two random variables are jointly distributed if they are both defined on the same probability space.
Definition :
A random vector
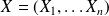is a maping from
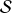to
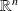for which all the components
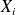are jointly distributed. The joint probability distribution is given for
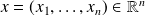by
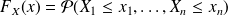
Definition :
The components
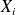are independent if the joint probability distribution is the product of the cumulative distributions, i.e.
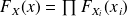
Definition :
A random vector
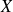has the joint probability density function if
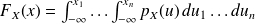
Definition :
The mean or expected value of a random vector
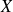is the vector
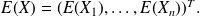
The covariance matrix is the
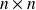matrix
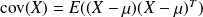
where
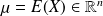ie.
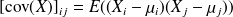
All covariance matrices in this lecture are assumed symmetric and positive definite !
Example :
A random vector has a Gaussian (or Normal) distribution if its joint probability density function is
.
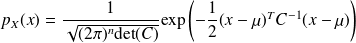one has
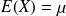
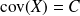
Notation :
