Rapport statistique sur la banque publique de l'épreuve orale de mathématiques des CCP, filière MP
André ANTIBI et Ludovic d'ESTAMPES, 2012 |
|---|
Introduction
Le document que nous présentons est un rapport de jury d'un type particulier, nouveau. En effet, il concerne une liste d'exercices « balayant » tout le programme de mathématiques de classes préparatoires MP, et dont les élèves avaient connaissance.
Il ne s'agit pas de nous substituer aux enseignants de ces classes, qui ont en charge la formation des élèves. Il s'agit pour nous de fournir un retour sur l'enseignement des mathématiques de ces classes et sur le travail et le niveau des candidats.
Cet échange entre collègues nous semble fructueux et de nature à améliorer l'enseignement en classes préparatoires, mais aussi dans les écoles d'ingénieurs qui peuvent ainsi disposer de renseignements utiles pour mieux s'adapter aux élèves de leurs écoles.
Quelques conclusions générales
N.B. : Il nous a semblé plus explicite de ramener les notes sur 8 à des notes sur 20, plus familières.
Les notes sont analogues à la session 1 (13,75 de moyenne) et à la session 2 (13,38 de moyenne).
Les moyennes des notes sont bonnes (moyenne générale de 13,67), mais pas excellentes, comme certains auraient pu s'y attendre. En effet, compte-tenu du grand nombre d'exercices, il ne suffit pas d'essayer de les mémoriser pour les restituer parfaitement.
On peut noter que les moyennes des notes en algèbre-géométrie (14,2) est supérieure à celle des notes d'analyse (13,13).
La valeur des écart-types en algèbre-géométrie (5,53) et en analyse (5,71) montrent clairement que les notes restent étalées. En d'autres termes, ce type d'évaluation permet de classer les candidats, mais dans ce cas, ce classement s'appuie essentiellement sur le travail et le niveau de compréhension des élèves.
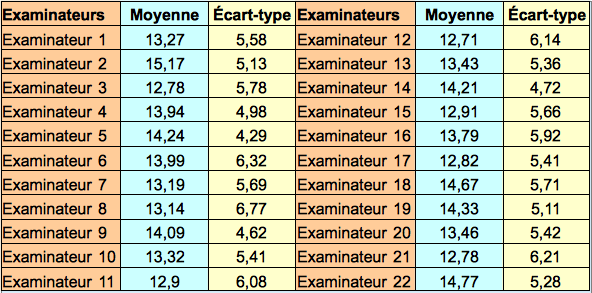
Comme l'indique le tableau 1 suivant, il n'y a pas de gros écarts dans les moyennes obtenues par les différents examinateurs. Un barème précis, pour chaque exercice, a été fourni. Lorsque la banque n'est pas publique, les écarts entre les moyennes obtenues par les différents examinateurs sont plus importants, malgré l'existence d'un barème.
Quelques conclusions relatives aux parties du programme
Nous avons regroupé les 120 exercices en sous-ensembles correspondants aux différentes parties du programme.
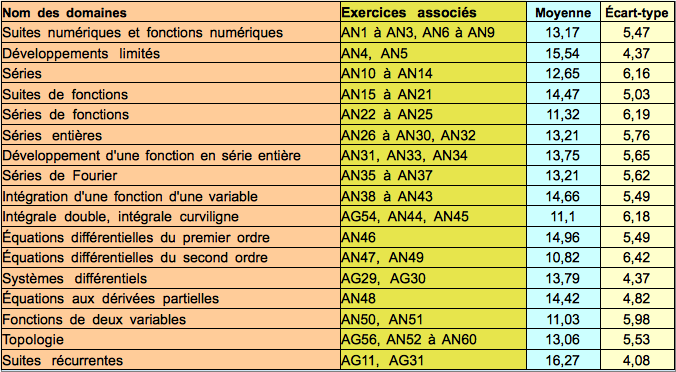
Plus précisément, nous avons fait le découpage suivant (voir le tableau 2 pour l'algèbre-géométrie et le tableau 3, page suivante, pour l'analyse).
Dans chacun de ces 28 domaines, la moyenne des notes est supérieure à 10/20, ainsi dans chacune de ces parties, les moyennes sont convenables. Ceci semble montrer que, en général, les étudiants n'ont pas fait d'impasses dans leurs préparations.
Algèbre-géométrie
Les connaissances de base en algèbre linéaire semblent particulièrement bien assimilées.
Plus généralement, les résultats sont convenables en algèbre, même pour la partie « structures », qui peut paraître trop abstraite.
En géométrie au contraire, les résultats sont moins bons. Cette situation vient probablement du fait que dès l'enseignement secondaire déjà, ce domaine d'enseignement n'est pas suffisamment pris en compte dans les programmes officiels.
On a cru bon de séparer la construction des courbes planes et l'étude locale d'une courbe ; dans ce dernier domaine, les élèves éprouvent davantage de difficulté.
Analyse
Parmi les domaines les moins bien réussis, dans deux d'entre eux les exercices nécessitent des connaissances de géométrie : « intégrale double et curviligne » et « fonctions de deux variables ».
Les élèves rencontrent des difficultés concernant l'étude des équations différentielles du second ordre : variation des constantes, obtention d'une solution générale quand on connaît une solution particulière, ...
Les élèves sont moins à l'aise pour manipuler des séries de fonctions que les suites de fonctions.
Les résultats obtenus dans le domaine des séries entières et des développements en séries entières sont tout-à-fait analogues à ceux obtenus sur les développements en séries de Fourier.
Quelques remarques sur la relation avec le système d'évaluation par contrat de confiance
Ce système d'évaluation des élèves mis en pratique à la session 2012 est le système d'évaluation par contrat de confiance (EPCC). Ce système est utilisé par plus de 30000 enseignants en France, dans les contrôles de connaissance, tout au long de l'année. Mais cette fois, pour le concours CCP, le programme de révision est beaucoup plus important.
La mise en application de ce système est encouragé au plus haut niveau : circulaire de rentrée de la Direction Générale des Enseignements Scolaires (DGESCO) en 2011-2012 ; rapport de l'Assemblée Nationale de Jacques Grosperrin sur le socle commun. Un article a été consacré à ce sujet dans la revue de la Conférence aux Grandes Ecoles (CGE). André Antibi a été invité à faire une conférence plénière, le 4 octobre 2012, lors du colloque de Nantes de la CGE ([1]).
Les principaux avantages du système EPCC se retrouvent dans notre étude :
Mis en confiance et guidés dans leurs révisions, les élèves travaillent davantage.
Il y a une diminution sensible du facteur chance.
Le travail est récompensé.
Signalons enfin que ce système ne permet pas à tous les élèves d'obtenir de très bonnes notes. Cela ressort clairement de notre étude. Les notes restent étalées.
Références et webographie
[1] André ANTIBI (2012), La constante macabre, Conférence plénière introductive, Congrès de Nantes de la CGE, 3-5 octobre 2012, pp. 23-25
[2] "Mouvement Contre La Constante Macabre" : http://mclcm.free.fr/