Intégration par parties
Théorème
Fondamental : Théorème
et 
sont deux fonctions dérivables sur un intervalle 
et telles que 
et 
soient continues sur . Pour tous réels 
et 
de , on a :
et étant dérivables sur , la fonction 
est dérivable sur et 
et étant continues sur , les fonctions 
et 
et par suite la fonction 
sont continues sur , on peut donc intégrer chaque membre de cette égalité entre et .
On écrit 
Donc 
et donc
car est une primitive de
Exemple
Exemple :
Calculer 
; 
avec (
)
Calcul de
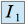: on pose 
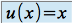et 
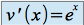,on obtient
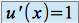et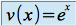 
donc
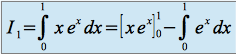
donc
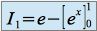
enfin
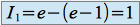
Calcul de
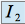: pour tout 
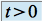, on pose 
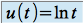et 
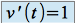,on obtient
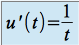et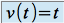 
donc
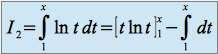
donc
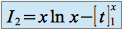
enfin
