Propriétés de majoration
Fondamental :
Soient 
et 
deux fonctions telles que 
Si
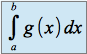converge, alors 
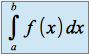converge.Si
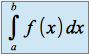diverge, alors 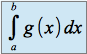diverge.
Exemple :
est intégrable sur 
En effet, on a la majoration 
et 
est intégrable sur .
par contre, cet argument ne donne pas la valeur de 
.
Fondamental :
Soient et deux fonctions telles que 
Si
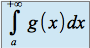converge, alors 
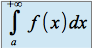converge.Si
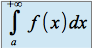diverge, alors 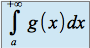diverge
Exemple :
et 
donc 
converge.
