Définition
Introduction
Nous n'avons utilisé, jusqu'ici que des intégrales du type ![]() , où
, où ![]() est intégrable au sens de Riemann, donc bornée sur
est intégrable au sens de Riemann, donc bornée sur ![]() . Abordons maintenant les deux situations suivantes, dans lesquelles on parle d'intégrales généralisées d'une fonction
. Abordons maintenant les deux situations suivantes, dans lesquelles on parle d'intégrales généralisées d'une fonction ![]() :
:
Quand on intègre sur un intervalle
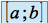 avec
avec 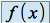 qui tend vers
qui tend vers  quand
quand 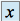 tend vers
tend vers 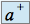 (c.a.d.
(c.a.d. 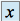 tend vers
tend vers  en restant supérieur à
en restant supérieur à  ) ou quand
) ou quand 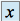 tend vers
tend vers 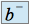 (notion symétrique) ou bien même quand
(notion symétrique) ou bien même quand 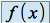 n'a pas de limite.
n'a pas de limite.Par exemple
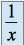 sur
sur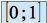 ,
, 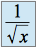 sur
sur 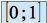 ,
, 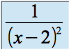 sur
sur  ,
, 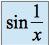 sur
sur 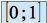 .
.ou bien quand on intègre sur un intervalle non borné du type
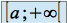 ,
, 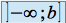 ou
ou 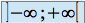 .
.Par exemple
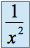 sur
sur 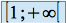 ,
, 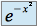 sur
sur 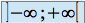 .
.
Pour simplifier la présentation, on se place systématiquement sur ![]() , ou sur
, ou sur ![]() , les adaptations à des intervalles différents mais du même type se font aisément.
, les adaptations à des intervalles différents mais du même type se font aisément.
Définition
On dit que la fonction
 n'ayant pas de limite en
n'ayant pas de limite en  est intégrable sur
est intégrable sur 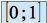 ou que l'intégrale généralisée converge en
ou que l'intégrale généralisée converge en  ou encore que la fonction est intégrable au voisinage de
ou encore que la fonction est intégrable au voisinage de  si et seulement si
si et seulement si 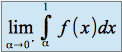 existe et est finie
existe et est finieet on pose
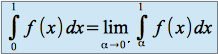
On dit que la fonction
 est intégrable sur
est intégrable sur 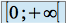 ou que l'intégrale généralisée converge en
ou que l'intégrale généralisée converge en 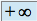 ou encore que la fonction est intégrable au voisinage de
ou encore que la fonction est intégrable au voisinage de 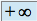 si et seulement si
si et seulement si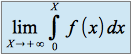 existe et est finie
existe et est finieet on pose
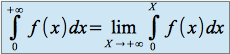
Lorsqu'une intégrale généralisée ne converge pas, on dit aussi qu'elle diverge.
Remarque :
Si l'on veut étudier l'intégrabilité de ![]() sur
sur ![]() on a deux problèmes de convergence : en
on a deux problèmes de convergence : en ![]() puisque
puisque ![]() et en
et en ![]() . On découpe l'intégrale en deux et on étudie séparément la convergence de
. On découpe l'intégrale en deux et on étudie séparément la convergence de ![]() et de
et de ![]() la valeur intermédiaire
la valeur intermédiaire ![]() étant arbitraire et n'ayant aucune influence sur la convergence de chaque morceau.
étant arbitraire et n'ayant aucune influence sur la convergence de chaque morceau.
Exemples
Exemple :
![]() est intégrable sur
est intégrable sur ![]()
En effet ![]() et
et ![]()
Donc
![]()
Exemple :
![]() converge
converge
On a : ![]() et
et ![]()
Donc
![]()
Exemple :
![]() est intégrable au voisinage de
est intégrable au voisinage de ![]() pour
pour ![]()
Pour ![]() une primitive de
une primitive de ![]() est
est ![]() on a donc
on a donc
![]()
Si
 on a
on a 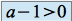 et donc
et donc 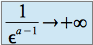 quand
quand 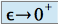 et l'intégrale diverge.
et l'intégrale diverge.Pour
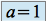 on a
on a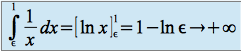 quand
quand  .
.Si
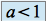 on a
on a 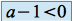 et
et 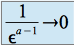 quand
quand  et l'intégrale converge et vaut
et l'intégrale converge et vaut
![]()
Sur ![]() le calcul est le même avec
le calcul est le même avec ![]() remplacé par
remplacé par ![]() avec
avec ![]() qui tend vers l'infini, ce qui inverse les cas de convergence. Calcul à faire à titre d'exercice.
qui tend vers l'infini, ce qui inverse les cas de convergence. Calcul à faire à titre d'exercice.
Commentaires
Remarque :
D'après ce que l'on vient de voir ![]() converge alors que
converge alors que ![]() diverge. Dans les deux cas la fonction que l'on intègre tend vers l'infini quand
diverge. Dans les deux cas la fonction que l'on intègre tend vers l'infini quand ![]() tend vers
tend vers ![]() . Mais
. Mais ![]() tend trop vite vers l'infini pour que l'intégrale converge. Ceci prend tout son sens si l'on se souvient que l'intégrale mesure (la fonction étant positive) l'aire du domaine compris entre la courbe et l'axe des
tend trop vite vers l'infini pour que l'intégrale converge. Ceci prend tout son sens si l'on se souvient que l'intégrale mesure (la fonction étant positive) l'aire du domaine compris entre la courbe et l'axe des ![]() . La fonction
. La fonction ![]() tend assez lentement vers l'infini pour que l'aire soit finie, même si une branche est infinie, alors que c'est faux pour
tend assez lentement vers l'infini pour que l'aire soit finie, même si une branche est infinie, alors que c'est faux pour ![]() .
.
La façon de tendre vers l'infini est donc ce qui importe pour la convergence de l'intégrale.





