Intégrale d'une fonction en escalier sur un segment
Définition : (Subdivision d'un intervalle)
On appelle subdivision d'un intervalle 
toute famille finie 
, telle que :
Définition : (Fonction en escalier)
Soit 
une fonction réelle de l'intervalle 
dans 
. est une fonction en escalier si et seulement si il existe une subdivision de , dite subdivision adaptée à
, telle que soit constante sur chacun des intervalles 
(pour tout 
de , on a 
, où 
est une constante réelle)
Remarque :
Les valeurs de aux points 
sont quelconques.
Remarque :
On note
l'ensemble des fonctions en escalier sur
Définition : (Intégrale d'une fonction en escalier)
Soit une fonction en escalier sur on appelle intégrale de sur le réel :
où est une subdivision adaptée à
Remarque :
Le réel
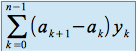ne dépend pas de la subdivision adaptée à
L'intégrale de
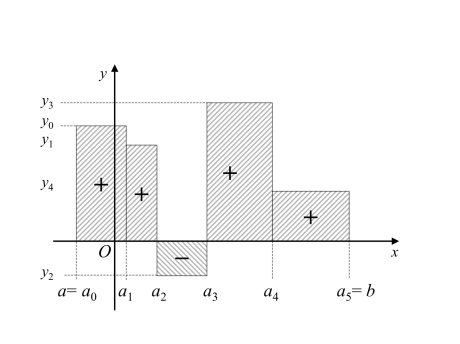
sur 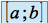est l'aire algébrique des rectangles hachurés de la figure qui suit : on affecte l'aire des rectangles situés au dessus de l'axe 
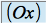d'un signe positif et l'aire de ceux situés en dessous de l'axe d'un signe négatif.
