Bilan
Introduction
Faisons maintenant apparaître des structures très fréquentes dans l'univers mathématique.
Groupe
Définition : Groupe
Soit 
un ensemble muni d'une loi de composition interne, 
. On dit que 
a une structure de groupe si la loi est associative (A), s'il existe dans un élément neutre (N), et si tout élément de admet un symétrique (S) (le symétrique de 
se note 
quand la loi est notée multiplicativement).
Si de plus la loi est commutative (C) alors le groupe est dit commutatif ou Abélien.
Calculs dans un groupe :
L'élément neutre est unique.
Le symétrique de
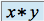est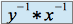 
.Si
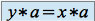alors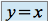 
(je peux simplifier par 
).
Exemple :
Anneau
Définition : Anneau
Soit 
un ensemble muni de deux lois internes, 
et . Si 
est un groupe commutatif, et si loi est associative et distributive par rapport à la loi , alors 
est un anneau.
Si, de plus, admet un élément neutre, alors est un anneau unitaire.
Si, de plus, est commutative, alors est un anneau commutatif.
Si, de plus, admet un élément neutre et est commutative, alors est un anneau unitaire commutatif.
Exemple : d'anneaux
; 
qui est l'ensemble des polynômes à coefficients réels.
Corps
Définition : Corps
On appelle corps, tout ensemble 
muni de deux lois internes, et , tel que :
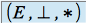est un anneau unitairetout élément de
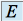, sauf le neutre de la première loi , admet un élément symétrique pour la deuxième loi .
Si, de plus, la deuxième loi est commutative, le corps est dit commutatif. (c'est sur ce type de corps que nous travaillerons.)
Exemple :
et 
sont des corps, 
aussi.
