Approche de la notion de groupe
Vous connaissez l'ensemble des nombres entiers naturels 
. Avec deux nombres entiers naturels, il est possible de calculer un nouvel entier, à savoir leur somme qui est toujours dans : par exemple, 
.
A l'aide du couple 
de 
on a construit un nouveau nombre 
qui appartient à .
Ceci étant vrai pour tout couple de nombres entiers, on dit alors que : + est une loi interne dans . Or cette loi a des propriétés importantes :
Vous savez que : 
Ceci étant vrai dans tous les cas, on écrit
,
et on dit que la loi + a la propriété de commutativité notée (C).
Vous savez aussi que 
. Ceci étant vrai dans tous les cas, on écrit
,
et on dit que la loi + a la propriété d'associativité notée (A) (Dans cette somme, la place des parenthèses ne change pas le résultat).
Vous savez enfin que : 
. Ceci étant vrai dans tous les cas, on écrit
,
et on dit que la loi + possède un élément neutre 0. Cette propriété sera notée (N).
En résumé, on dira que : 
possède les propriétés : (C, A, N).
Dans , on ne peut pas résoudre l'équation d'inconnue 
: 
car l'opposé de 2 n'existe pas dans , d'où la nécessité d'introduire de nouveaux nombres, les entiers relatifs : 
.
Dans , on peut définir l'addition, qui est une loi interne, et pour laquelle 
possède aussi les propriétés (C, A, N). En outre, l'équation précédente peut se résoudre dans . Par exemple 
, (
est l'opposé de 
pour l'addition).
Plus généralement, on dit que est le symétrique de pour la loi + . Ceci étant vrai dans tous les cas, on écrit
et on dit que tout élément de possède un symétrique dans . Cette propriété sera notée (S).
En résumé, on dira que possède les propriétés : (C, A, N, S).
Définition :
Soit un ensemble 
. Toute une application 
de 
dans est appelée loi de composition interne dans un ensemble .
Définition : Propriétés d'une telle loi
Associativité :
est associative si : 
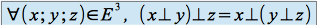. S'il en est ainsi, les parenthèses sont inutiles et on écrira simplement 
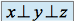.Commutativité :
est commutative si : 
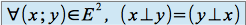.Élément neutre : Il existe un élément
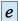de 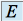tel que 
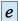. est appelé un élément neutre de la loi .Symétrique : Un élément
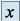de 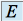admet un symétrique pour la loi s'il existe un élément 
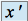de 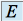tel que 
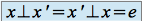. Si tout élément de
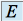admet un symétrique dans 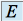, on dit que la loi possède la propriété .
