Approche de la notion d'anneau et de corps
Dans 
, il existe une deuxième loi interne : la multiplication que nous noterons 
. Cette loi possède les propriétés (C, A, N) (le neutre étant 1), mais pas (S). En effet, aucun entier relatif n'est solution, par exemple, de l'équation 
. (Ceci nécessite la création d'un ensemble
"plus grand'' contenant; Il s'agit de l'ensemble 
des nombres rationnels).
Lorsque, dans un ensemble il existe deux lois, on peut les faire opérer l'une avec l'autre :
Ainsi, vous savez que
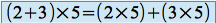. Si ceci est vrai dans tous les cas, on parle alors de distributivité à droite de la multiplication par rapport à l'addition.De même, il existe la distributivité à gauche. Dans l'exemple précédent, on écrirait
.
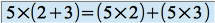Si la deuxième loi est distributive à droite et à gauche par rapport à la première loi, on dit simplement qu'il y a distributivité, propriété notée (D).
Cela signifie, pour un ensemble 
muni des opétations 
et 
:
