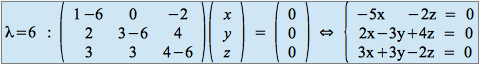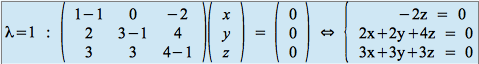Recherche des vecteurs propres
Méthode :
Après avoir déterminé les racines du polynôme caractéristique d'un endomorphisme 
, on peut passer à la recherche des vecteurs propres de . Pour chaque valeur propre 
, on détermine une base du sous espace vectoriel 
en résolvant le système linéaire :
, 
est le vecteur que l'on cherche, ses coordonnées sont les inconnues du système à résoudre.
étant la représentation matricielle de dans une base donnée. La résolution de ce système nous donnera alors les coordonnées dans cette même base des vecteurs propres de associés à la valeur propre .
Exemple :
Reprenons le dernier exemple de la section précédente, dans lequel on avait déterminé deux racines réelles du polynôme caractéristique, 
et 
. Calculons les vecteurs propres associés :
.
.
Ainsi, les deux sous-espaces propres, 
et 
, sont tous deux de dimension 1, et engendrés respectivement par les vecteurs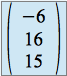 
et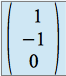 
.
Remarque :
Dans cet exemple, la réunion des bases de et n'engendre pas 
en entier, mais seulement un sous espace vectoriel de dimension 2 dans . On ne pourra donc pas introduire de changement de base qui permettrait de DIAGONALISER l'endomorphisme .
