Le polynôme caractéristique d'un endomorphisme
Soit 
un 
-espace vectoriel de dimension finie. Soit 
un endomorphisme de , et soit 
une valeur propre de . Il existe alors un vecteur propre 
(non nul) tel que 
ou encore 
. Ainsi, 
n'est pas injectif, ce qui en dimension finie se traduit par
.
Si on note 
la matrice de l'endomorphisme dans une base 
de , ceci s'écrit aussi
,
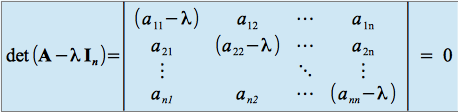la valeur de ce déterminant étant indépendante du choix de la base puisque le déterminant est invariant par transformation de similitude.
Définition :
Soit un -espace vectoriel de dimension 
, et soit un endomorphisme de . On appelle polynôme caractéristique de , le polynôme
.
Ce polynôme est indépendant de la base de la base choisie dans laquelle on exprime le déterminant, et il est de degré en
Fondamental : Propriété
Soit un -espace vectoriel de dimension finie. Soit un endomorphisme de , et soit 
le polynôme caractéristique de .
L'ensemble des racines de
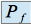, quand elles existent, constitue le spectre de 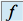.Pour toute racine
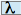de (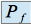
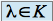), le sous espace propre associé correspond à : 
.
On a aussi le résultat suivant :
Fondamental : Propriété
Soit un-espace vectoriel de dimension finie, et soit un endomorphisme de . Si est une valeur propre de , racine de multiplicité 
du polynôme caractéristique de , alors :
.
Enfin, il faut noter le résultat fondamental suivant :
Fondamental : Théorème
Soit un -espace vectoriel de dimension finie. Soit un endomorphisme de , et soit le polynôme caractéristique de . Alors est un polynôme annulateur de , c'est à dire que 
est égal à l'endomorphisme nul de et que, pour toute représentation matricielle 
de dans une base donnée de ,
.
