Systèmes d'équations linéaires
Système triangulaire
Soit le système :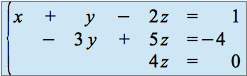 
où 
, 
et 
sont les inconnues.
Résoudre un tel système est aisé : on résout la dernière équation, puis la seconde en reportant la valeur de puis la première en reportant les valeurs de et .
Un tel système est dit "triangulaire". Il admet une seule solution : le triplet 
Mise en oeuvre de la méthode de Gauss
Méthode :
Résoudre le système :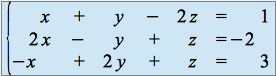
Il faut, pour cela, se ramener à un système triangulaire en effectuant des opérations sur les lignes (un système linéaire a même ensemble de solutions que le système obtenu en remplaçant une ligne par une combinaison linéaire de cette ligne et d'une autre ligne).
La méthode utilisée s'appelle "méthode du pivot de Gauss". On choisit la première ligne 
comme pivot, on remplace la deuxième ligne par 
(on multiplie les deux membres de par 
pour avoir le même coefficient de que dans 
, puis on soustrait à , ce qui annule le coefficient de ), et on remplace la dernière ligne par 
pour la même raison.
On obtient :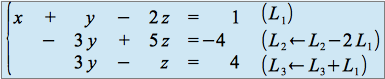
Il reste à "éliminer" en remplaçant la dernière ligne par 
.
On obtient finalement :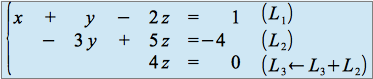
Le système obtenu est triangulaire, l'ensemble des solutions est 
