Exemples
Exemple :
Soit ![]() l'endomorphisme dans
l'endomorphisme dans ![]() , de matrice
, de matrice  . Son polynôme caractéristique,
. Son polynôme caractéristique, ![]() , n'est pas scindé dans
, n'est pas scindé dans ![]() et
et ![]() n'est donc pas diagonalisable dans le
n'est donc pas diagonalisable dans le ![]() -espace vectoriel
-espace vectoriel ![]() .
.
Par contre, ![]() est scindé sur
est scindé sur ![]() , et possède trois racines simples (
, et possède trois racines simples (![]() , et
, et ![]() ) et on peut donc dire que
) et on peut donc dire que ![]() est diagonalisable dans le
est diagonalisable dans le ![]() -espace vectoriel
-espace vectoriel ![]() (qui contient
(qui contient ![]() ). Cependant, pour mettre
). Cependant, pour mettre ![]() sous forme diagonale dans
sous forme diagonale dans ![]() , il faut utiliser un changement de base à coefficients dans
, il faut utiliser un changement de base à coefficients dans ![]() et non dans
et non dans ![]() .
.
Exemple :
Soit l'endomorphisme dans ![]() de matrice
de matrice ![]() . Son polynôme caractéristique est
. Son polynôme caractéristique est ![]() , qui est bien scindé dans
, qui est bien scindé dans ![]() , et le sous-espace propre associé est
, et le sous-espace propre associé est
![]() .
.
Comme il n'y a pas d'autre vecteur propre linéairement indépendant de celui-ci qui soit associé à la valeur propre 1, le sous-espace propre ![]() n'est que de dimension 1 et la condition 2 n'est pas vérifiée. En conclusion
n'est que de dimension 1 et la condition 2 n'est pas vérifiée. En conclusion ![]() n'est pas diagonalisable dans
n'est pas diagonalisable dans ![]() .
.
Pour les même raisons, il ne le serait pas non plus dans ![]() .
.
Remarque :
Pour savoir si un endomorphisme ![]() est diagonalisable, il suffit de déterminer ses valeurs propres, leur multiplicité, et le rang de
est diagonalisable, il suffit de déterminer ses valeurs propres, leur multiplicité, et le rang de ![]() pour chaque valeur propre.
pour chaque valeur propre.
Exemple :
Soit  , et
, et ![]() .
. 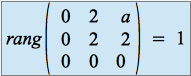 si
si ![]() , et 2 si
, et 2 si ![]() . Que conclure?
. Que conclure?
Réponse
1 est valeur propre double de ![]() , donc pour que
, donc pour que ![]() soit diagonalisable, il faut que la dimension du sous espace propre associé à la valeur propre 1 soit 2.
soit diagonalisable, il faut que la dimension du sous espace propre associé à la valeur propre 1 soit 2.
D'après le théorème du rang, il faut donc que ![]() , ce qui n'est réalisé que pour
, ce qui n'est réalisé que pour ![]() . De plus, la valeur propre 3 étant simple, la dimension de son espace propre est obligatoirement 1 (en effet :
. De plus, la valeur propre 3 étant simple, la dimension de son espace propre est obligatoirement 1 (en effet : ![]() = multiplicité de la valeur propre 3).
= multiplicité de la valeur propre 3).
En conclusion : si ![]() ,
, ![]() est diagonalisable, sinon elle ne l'est pas.
est diagonalisable, sinon elle ne l'est pas.





