Endomorphisme diagonalisable
Définition :
Soit ![]() un
un ![]() -espace vectoriel de dimension finie, et soit
-espace vectoriel de dimension finie, et soit ![]() un endomorphisme de
un endomorphisme de ![]() . On dit que
. On dit que ![]() est DIAGONALISABLE si et seulement si il existe une base de
est DIAGONALISABLE si et seulement si il existe une base de ![]() dans laquelle la matrice de
dans laquelle la matrice de ![]() est diagonale.
est diagonale.
Exemple :
On a pu précédemment vérifier que l'endomorphisme ![]() associé à la matrice
associé à la matrice ![]() est diagonalisable dans
est diagonalisable dans ![]() .
.
Fondamental : Théorème
Soit ![]() un
un ![]() -espace vectoriel de dimension finie. Un endomorphisme
-espace vectoriel de dimension finie. Un endomorphisme ![]() de
de ![]() est diagonalisable si et seulement si il existe une base de
est diagonalisable si et seulement si il existe une base de ![]() formée de vecteurs propres de
formée de vecteurs propres de ![]() .
.
Fondamental : Théorème
Soit ![]() un
un ![]() -espace vectoriel de dimension finie. Un endomorphisme
-espace vectoriel de dimension finie. Un endomorphisme ![]() de
de ![]() est diagonalisable si et seulement si
est diagonalisable si et seulement si ![]() est somme directe d'espaces propres de
est somme directe d'espaces propres de ![]() .
.
On a aussi :
Fondamental : Propriété
Soit ![]() un
un ![]() -espace vectoriel de dimension
-espace vectoriel de dimension ![]() . Si
. Si ![]()
![]() , sont les
, sont les ![]() valeurs propres distinctes d'un endomorphisme
valeurs propres distinctes d'un endomorphisme ![]() de
de ![]() , alors
, alors ![]() est diagonalisable dans
est diagonalisable dans ![]() si et seulement si
si et seulement si
![]() ou encore
ou encore ![]() .
.
Fondamental : Théorème fondamental
Soit ![]() un
un ![]() -espace vectoriel de dimension finie. Un endomorphisme
-espace vectoriel de dimension finie. Un endomorphisme ![]() de
de ![]() est diagonalisable si et seulement si il vérifie les deux conditions suivantes :
est diagonalisable si et seulement si il vérifie les deux conditions suivantes :
son polynôme caractéristique
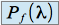 est scindé dans le corps
est scindé dans le corps 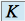 de référence (c'est à dire que
de référence (c'est à dire que 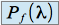 est factorisable en facteurs du
est factorisable en facteurs du  degré à coefficients dans
degré à coefficients dans 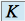 )
)pour chaque valeur propre
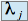 de multiplicité
de multiplicité 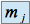 , on a
, on a 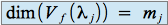 .
.
Remarque :
Dans
 , la condition 1 est automatiquement vérifiée.
, la condition 1 est automatiquement vérifiée.Si
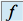 est diagonalisable, la restriction de
est diagonalisable, la restriction de 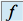 à chacun de ses sous espaces propres est soit l'application nulle, si la valeur propre correspondante est nulle, soit une homothétie de rapport égal à la valeur propre correspondante.
à chacun de ses sous espaces propres est soit l'application nulle, si la valeur propre correspondante est nulle, soit une homothétie de rapport égal à la valeur propre correspondante.Un cas particulier important car assez fréquent est le suivant : Soit
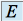 un
un 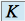 -espace vectoriel de dimension
-espace vectoriel de dimension  . Si un endomorphisme
. Si un endomorphisme 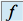 de
de 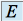 a
a  valeurs propres distinctes chacune de multiplicité 1 alors cet endomorphisme est diagonalisable.
valeurs propres distinctes chacune de multiplicité 1 alors cet endomorphisme est diagonalisable.





