Déterminant de matrices ℳ₃(ℝ)
Méthode :
Dans ![]() , le déterminant d'une matrice
, le déterminant d'une matrice ![]() ,
, 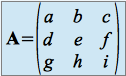 , est donné par le réel
, est donné par le réel
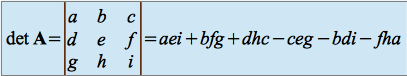 .
.
Fondamental : Propriétés
On retrouve là encore des propriétés tout à fait similaires, à savoir :
Le déterminant d'une matrice
 est une application tri-linéaire, c'est à dire linéaire par rapport à chacune des trois colonnes ou vecteurs de
est une application tri-linéaire, c'est à dire linéaire par rapport à chacune des trois colonnes ou vecteurs de  dans cette matrice.
dans cette matrice.Le déterminant d'une matrice
 est une application alternée, c'est à dire que si on échange deux colonnes quelconques entre elles dans la matrice, le déterminant change de signe.
est une application alternée, c'est à dire que si on échange deux colonnes quelconques entre elles dans la matrice, le déterminant change de signe.Le déterminant est nul si et seulement si les vecteurs colonne de la matrice sont colinéaires (ne forment pas une famille libre).
Le déterminant d'une matrice
 est égal à celui de sa transposée.
est égal à celui de sa transposée.Le déterminant du produit de deux matrices
 est égal au produit des deux déterminants de chacune des deux matrices.
est égal au produit des deux déterminants de chacune des deux matrices.





