Déterminant de matrices ℳ₂(ℝ)
Introduction
Le déterminant est une application qui, à toute matrice de 
, associe un réel. L'intérêt des déterminants est de fournir des conditions explicites pour étudier l'indépendance linéaire.
Méthode :
Dans 
, le déterminant d'une matrice 
, 
, est donné par le réel 
, c'est à dire par la différence entre le produit des termes de la diagonale principale et le produit des termes de la diagonale transverse. On le note :
Le déterminant de la matrice 
, 
, est aussi appelé déterminant de la famille de vecteurs
et noté 
.
Fondamental : Propriétés
Il est facile de vérifier les propriétés suivantes :
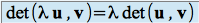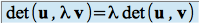
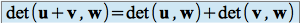et 
et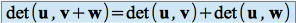 
En résumé, on dit que l'application qui à tout couple de vecteurs de
associe son déterminant, est une application bilinéaire (propriétés 1 et 2) alternée (propriété 3).On peut aussi démontrer que :
si et seulement si les vecteurs 
et 
sont colinéaires (ne forment pas une famille libre).Le déterminant d'une matrice
est égal à celui de sa transposée
Le déterminant du produit de deux matrices
est égal au produit des deux déterminants
