Fonction de distribution radiale
Définition : Fonction de distribution radiale
Fluide isotrope :
Dans un fluide isotrope, il n'y a pas de dépendance angulaire du potentiel d'interaction VN. On peut alors déplacer l'origine d'observation de la propriété sans affecter sa valeur. Ainsi, la corrélation entre deux corps de positions r1 et r2 peut s'exprimer en fonction de leur distance : r12= |r1-r2| :
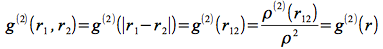
c'est la fonction de distribution radiale ou encore la fonction de corrélation de paires.
Fluide anisotrope :
même définition par convention.
Interprétation de la fonction de distribution radiale
En considérant une répartition homogène des particules dans l'espace, la fonction de distribution radiale g(2)(r) = g(r) représente la probabilité de trouver une particule dans l'écorce dr à la distance r d'une autre particule comme le montre la figure ci-dessous :
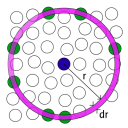
L'allure d'une courbe g(r) est caractéristique pour les liquides de celle présentée en dessous :
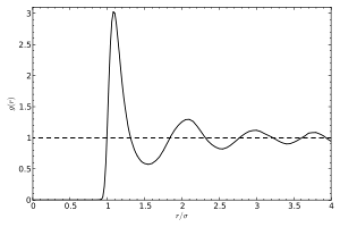
Remarque : propriétés de la fonction de distribution radiale
pour un liquide homogène et monoatomique décrit par un potentiel d'interaction de paire (ici Lennard Jones), la position des pics est espacée de façon régulière : pic à 1, 2, 3, ... diamètre atomiques
à longue distance, la valeur de g(r) tends vers 1.
Importance en thermodynamique de la fonction de distribution radiale g(r)
La fonction de distribution radiale g2(r) a une grande importance en thermodynamique :
On mesure expérimentalement pour les liquides et les solides, par diffraction de neutron, le facteur de structure, Sk, qui est la transformée de Fourier de g2(r).
On calcule g2(r) est calculable à partir de la connaissance d'un potentiel d'interaction VN(rN).
On peut déterminer g2(r) par simulation moléculaire (cf exemples dans les figures ci-dessous).
Par conséquent :
En comparant les mesures et le calcul, on peut s'en servir pour évaluer la pertinence d'un potentiel VN.
Nous allons voir plus loin dans le cours qu'il est également possible de calculer les autres grandeurs thermodynamiques à partir de g(r) qui intervient dans l'expression du second coefficient du viriel.





