IV.2 Modèle dynamique petit signal de la jonction PN [La jonction PN et ses applications]

IV.2 Modèle dynamique petit signal de la jonction PN

a) En polarisation directe

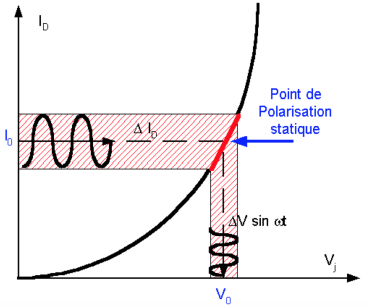
Fondamental :

On voit sur la figure que la diode est équivalente à une résistance de valeur $r_{d}$ appelée résistance dynamique.

Pour la déterminer, on dérive l'équation d'état de la diode autour du point de fonctionnement :

$r_{d} = {(\frac{dV}{dI})}_{I_{0}}$ .

Et on trouve, pour une diode franchement polarisée en direct :

Définition :

$r_{d} = \frac{U_{T}}{I_{0}}$

Remarque :

Ce modèle est valable à basse fréquence.

À haute fréquence, il faut prendre en compte les effets capacitifs dus aux porteurs minoritaires stockés dans les zones neutres :

On a vu que le courant qui circule dans une diode en direct est dû à la présence de porteurs minoritaires en excès qui diffusent

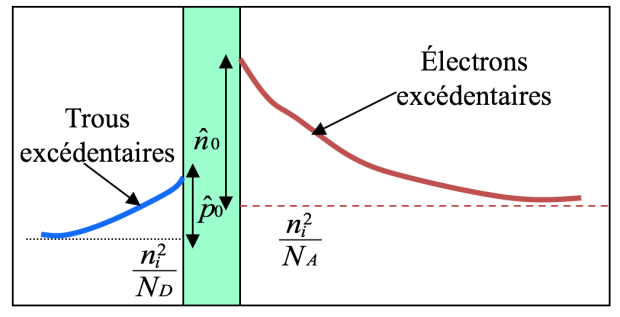
Si on intègre ces porteurs dans toute la zone neutre, on peut évaluer la charge correspondante $Q_{ZNN}$ dans la zone neutre N :

Q_{ZNN} = q A_{j} \int_{ZNN} \hat{p} dx = q A_{j} \frac{{\hat{p}}_{0}}{sh (\frac{W_{N}}{L_{p}})} \int_{ZNN} sh (\frac{W_{N} - x}{L_{p}}) dx

Considérons une jonction de type P⁺N. On a alors $Q \approx Q_{ZNN}$ . De plus si la ZNN est courte alors :

\begin{matrix} Q_{ZNN} = q A_{j} \frac{{\hat{p}}_{0}}{W_{N}} \int_{ZNN} (W_{N} - x) dx = q A_{j} \frac{{\hat{p}}_{0}}{W_{N}} {[W_{N} x - \frac{x^{2}}{2}]}_{0}^{W_{N}} \\ = q A_{j} \frac{{\hat{p}}_{0} W_{N}}{2} = q A_{j} \frac{W_{N}}{2} \bar{p} [\exp (\frac{V}{U_{T}}) - 1] \end{matrix}

On a $Q = \frac{I W_{N}^{2}}{2 D_{p}}$ et $C_{d} = \frac{dQ}{dV} = \frac{I_{s} W_{N}^{2}}{2 D_{p}} \frac{d}{dV} [\exp (\frac{V}{U_{T}})] = \frac{I_{s} W_{N}^{2}}{2 D_{p}} \exp (\frac{V}{U_{T}})$ .

On en déduit :

Définition :

$C_{d} = \frac{I W_{N}^{2}}{2 D_{P} U_{T}}$ .

b) En polarisation inverse

Résistance dynamique tend vers l'infini
Pas de capacité de stockage dans les zones neutres car le courant est très faible.
Apparition d'une capacité $C_{T}$ due à la largeur importante de la zce^[1] en polarisation inverse

Définition :

C_{T} = \frac{ϵ A_{j}}{δ} = \sqrt{\frac{q N^{*} ϵ}{2 (ϕ_{NP} - V)}} A_{j}

La zce^[1] équivaut à un diélectrique (pas de porteurs de charges à l'intérieur) de constante diélectrique $ϵ$ .

Fondamental : Conclusion

Le modèle de la diode en régime dynamique dépend de sa polarisation :

Ainsi, une diode polarisée en direct induit une constante de temps $τ$ telle que :

τ = C_{d} r_{d} = \frac{I W_{N}^{2}}{2 D_{P} U_{T}} \frac{U_{T}}{I} \Rightarrow τ = \frac{W_{N}^{2}}{2 D_{P}}