IV.1 Détermination du point de polarisation (ou point de fonctionnement) de la jonction [La jonction PN et ses applications]

IV.1 Détermination du point de polarisation (ou point de fonctionnement) de la jonction

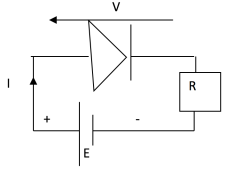
Résolution d'1 système à 2 équations, 2 inconnues :

${\begin{matrix} I & = & I_{s} [\exp (\frac{V}{U_{T}}) - 1] \\ E & = & R I + V \end{matrix} {\begin{matrix} E & = & 3 V \\ R & = & 100 Ω \\ I_{s} & = & 10^{- 12} A \end{matrix}$

3 solutions de résolution :

Méthode : 1- méthode approchée (la plus utilisée en circuit (notamment quand on ne connait pas Is)

On approxime la tension aux bornes de la diode à une tension $V_{T}$ appelée tension de seuil.

On considère que :

si $V < V_{T}$ , diode bloquée, $I = 0$ .
si la diode est passante, $V = V_{T}$ quel que soit $I$ .

Donc $I = \frac{E - V_{T}}{R}$ pour une diode au silicium.

Méthode : 2- méthode analytique par approximations successives

Elle est plus précise que la précédente mais nécessite de connaitre le courant de saturation de la diode.

Je considère que $V \approx 0,6 V$ .

Donc $I = (E - V) / R = (3 - 0,6) / 100 = 24 mA$ .

Donc $V = U_{T} Ln (I / I_{s} + 1) = 0,026 Ln (0,024 / 10^{- 12} + 1) = 0,621 V$ .

Donc $I = (E - V) / R = (3 - 0,621) / 100 = 23,8 mA$ .

Donc $V = U_{T} Ln (I / I_{s} + 1) = 0,026 Ln (0,0238 / 10^{- 12} + 1) = 0,621 V$ .

J'ai convergé. On a $I = 23,8 mA$ et $V = 0,621 V$ .

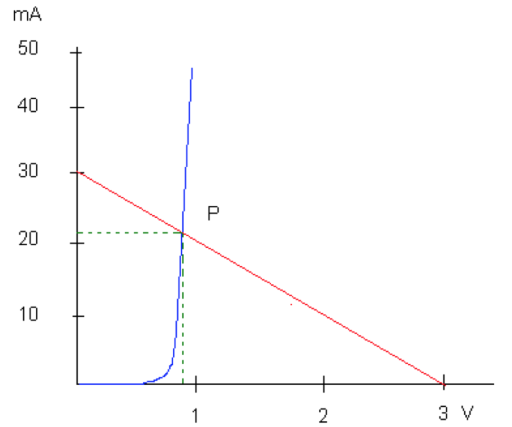
Méthode : 3- méthode graphique

Je trace les 2 équations du sytème à résoudre et, à leur intersection, se trouve le point de fonctionnement: