La jonction PN et ses applications

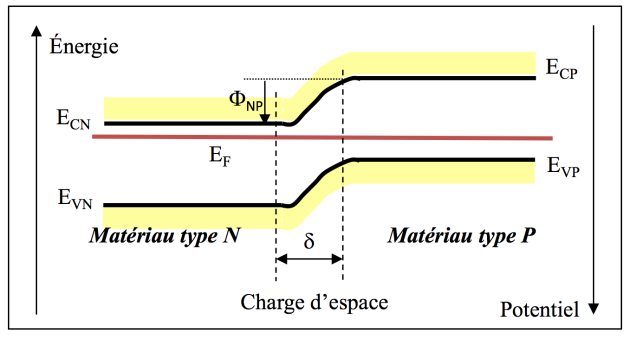
Pour déterminer la hauteur de la barrière de potentiel, nous allons nous référer à sa définition à partir des diagrammes d'énergie. Le schéma de bandes représenté ci-après montre que la hauteur de la barrière peut se déduire de la différence d'énergie des porteurs de même type de part et d'autre de la charge d'espace.

Or, les densités de porteurs sont directement liées aux énergies. Nous pouvons donc exprimer la densité des porteurs d'un même type de part et d'autre de la jonction.

L'expression des densités de porteurs s'écrit : $\overline{n}=N\exp \left(-\frac{E_C-E_F}{kT}\right)$

Si nous écrivons cette expression pour les électrons dans la région N et dans la région P, il vient :

• Région N : ${\overline{n}}_N=N\exp \left(-\frac{E_{\mathit{CN}}-E_F}{kT}\right)$

• Région P : ${\overline{n}}_P=N\exp \left(-\frac{E_{\mathit{CP}}-E_F}{kT}\right)$

Or : ${\mathrm{\Phi }}_{\mathit{NP}}={\mathrm{\Phi }}_N-{\mathrm{\Phi }}_P=-\frac{1}{q}(E_{\mathit{CN}}-E_{\mathit{CP}})$

On en tire : $E_{\mathit{CP}}=E_{\mathit{CN}}+q{\mathrm{\Phi }}_{\mathit{NP}}=E_{\mathit{CN}}+q({\mathrm{\Phi }}_N-{\mathrm{\Phi }}_P)$ .

En reportant cette valeur de $E_{\mathit{CP}}$ dans celle donnant la densité des électrons dans la région P, on obtient :

Ce qui donne : ${\overline{n}}_P={\overline{n}}_N\exp \left(-\frac{{\mathrm{\Phi }}_{\mathit{NP}}}{U_T}\right)$ dans lequel

Dans la région ou ils sont majoritaires, la densité des électrons vaut : $\overline{n_N}=N_D$

Dans celle ou ils sont minoritaires, cette densité devient : ${\overline{n}}_P=\frac{n_i^2}{N_A}$

En remplaçant dans l'expression qui fait intervenir Φ, on a : ${\overline{n}}_P={\overline{n}}_N\exp \left(-\frac{{\mathrm{\Phi }}_{\mathit{NP}}}{U_T}\right)\Rightarrow {\mathrm{\Phi }}_{\mathit{NP}}=U_T\text{Ln}\frac{{\overline{n}}_N}{{\overline{n}}_P}=U_T\text{Ln}\frac{N_A{N}_D}{n_i^2}$

Donc :