La jonction PN et ses applications

Pour définir les caractéristiques de la charge d'espace, nous allons utiliser des hypothèses connues sous le nom d'hypothèses de Schokley, qui s'énoncent sous la forme suivante :

• La charge d'espace est limitée par des plans parallèles au plan de la jonction métallurgique.

• La charge d'espace est dépourvue de porteurs libres

• Le champ est nul en dehors de la charge d'espace (donc le potentiel est constant).

Nous allons, pour établir les équations permettant de déterminer la hauteur et la largeur de la charge d'espace, utiliser le modèle défini à partir des hypothèses de Schokley. Nous considèrerons en outre que le matériau est homogène dans le plan $\mathit{YZ}$ et de ce fait, nous utiliserons un modèle unidimensionnel. La charge électrique qui existe dans la charge d'espace correspond donc à la représentation ci-dessous.

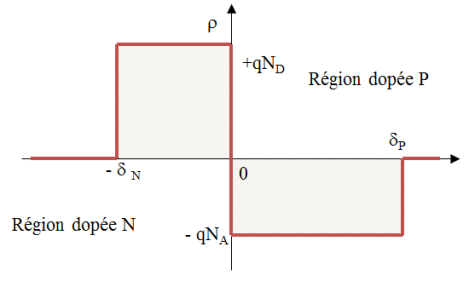
Entre la limite de charge d'espace côté N ($x=-{\mathrm{\delta }}_N$) et la position de la jonction métallurgique ($x=0$), on a une charge négative de valeur constante en fonction de la distance eu égard au dopage uniforme du matériau. Cette charge vaut : $\mathrm{\rho }=+q{N}_{D\mathrm{.}}$

De la même manière, coté P, entre la position de la jonction métallurgique et la limite de charge d'espace ($x={\mathrm{\delta }}_P$), la charge est constante et négative. Elle vaut : $\mathrm{\rho }=-{\mathit{qN}}_{A\mathrm{.}}$

Lorsque, dans un matériau, il existe une charge, on peut lui associer un potentiel grâce à l'équation de Poisson. Cette dernière s'écrit :

Dans le cas d'un modèle unidimensionnel, le Laplacien se ramène à une simple dérivée seconde et la relation s'écrira donc :

Pour $x$ compris entre $-{\mathrm{\delta }}_N$ et 0, la charge s'écrit : $\mathrm{\rho }=+q{N}_D$.

L'équation de poisson devient dans cette zone : $\frac{d^{2}V}{{\mathit{dx}}^2}=-\frac{q{N}_d}{\mathrm{ϵ}}$

L'intégrale première donne, au signe près, le champ électrique : $\frac{dV}{dx}=-q\frac{N_D}{\mathrm{ϵ}}x+C^{\mathit{te}}=-E$ soit $E=q\frac{N_D}{\mathrm{ϵ}}x+C^{\mathit{te}}\mathrm{.}$

La constante se détermine en écrivant que le champ électrique est nul à la limite de la charge d'espace, c'est-à dire pour $x=-{\mathrm{\delta }}_N$. Cela donne : $C^{\mathit{te}}=\frac{q{N}_D}{\mathrm{ϵ}}{\mathrm{\delta }}_N$

Le champ électrique s'écrit donc : $E=+\frac{q{N}_D}{\mathrm{ϵ}}(x+{\mathrm{\delta }}_N)$ soit $\frac{\mathit{dV}}{\mathit{dx}}=-\frac{q{N}_D}{\mathrm{ϵ}}(x+{\mathrm{\delta }}_N)$.

En intégrant une deuxième fois, on obtient : $V=-\frac{q{N}_D}{\mathrm{ϵ}}\left(\frac{x^2}{2}+x{\mathrm{\delta }}_N\right)+C^{\mathit{te}}\mathrm{.}$

La détermination de la constante d'intégration se fera aussi en utilisant les conditions aux limites: Le champ étant nul à l'extérieur de la zce, le potentiel qui en est l'intégrale première est constant. On le posera égal à ${\mathrm{\Phi }}_N$ dans la région N. Il s'en suit : $C^{\mathit{te}}=-\frac{q{N}_D}{\mathrm{ϵ}}\frac{{\mathrm{\delta }}_N^2}{2}+{\mathrm{\Phi }}_{N\mathrm{.}}$

En reportant dans l'expression du potentiel, on obtient : $V=-\frac{q{N}_D}{2\mathrm{ϵ}}{(x+{\mathrm{\delta }}_N)}^2+{\mathrm{\Phi }}_{N\mathrm{.}}$

Le même calcul fait entre 0 et ${\mathrm{\delta }}_P$ donnera des équations similaires. Il suffit de changer $-{\mathrm{\delta }}_N$ par  $+{\mathrm{\delta }}_P$ et  $+q{N}_D$ par $-q{N}_A$. On obtient, en posant que la tension dans la région P est égale à ${\mathrm{\Phi }}_P$ :

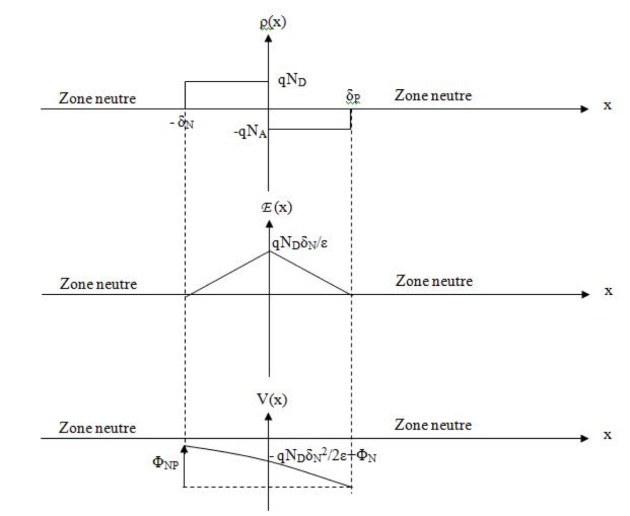
Si l'on représente sur un graphique la densité de charges, le champ électrique et le potentiel, on obtient finalement:

L'écriture de la continuité du potentiel en 0 donne : $V_{(0)}\Rightarrow \frac{q{N}_A}{2\mathrm{ϵ}}{(-{\mathrm{\delta }}_P)}^2+{\mathrm{\Phi }}_P=\frac{q{N}_A}{2\mathrm{ϵ}}{({\mathrm{\delta }}_N)}^2+{\mathrm{\Phi }}_N$ soit ${\mathrm{\Phi }}_N-{\mathrm{\Phi }}_P=\frac{q}{2\mathrm{ϵ}}(N_A{\mathrm{\delta }}_P^2+N_D{\mathrm{\delta }}_N^2)$ .

Pour simplifier l'écriture, on posera : ${\mathrm{\Phi }}_N-{\mathrm{\Phi }}_P={\mathrm{\varphi }}_{\mathit{NP}}$.

On obtient donc deux relations faisant intervenir ${\mathrm{\delta }}_N$ et ${\mathrm{\delta }}_P$. Il est donc facile de résoudre le système afin de calculer δ qui est la somme de ces deux termes.

L'équation (1) donne : $\frac{{\mathrm{\delta }}_P}{N_D}=\frac{{\mathrm{\delta }}_N}{N_A}=\frac{{\mathrm{\delta }}_P+{\mathrm{\delta }}_N}{N_A+N_D}=\frac{\mathrm{\delta }}{N_D+N_A}$ soit : ${\mathrm{\delta }}_P=\frac{\mathrm{\delta }{N}_D}{N_D+N_A}=\frac{\mathrm{\delta }}{N_A}\frac{N_A{N}_D}{N_D+N_A}$ et ${\mathrm{\delta }}_N=\frac{\mathrm{\delta }{N}_A}{N_D+N_A}=\frac{\mathrm{\delta }}{N_D}\frac{N_A{N}_D}{N_D+N_A}$ .

Pour des simplifications d'écriture, on pose : $N^{\text{*}}=\frac{N_A{N}_D}{N_A+N_D}$ .

L'équation (2) s'écrit alors : ${\mathrm{\varphi }}_{\mathit{NP}}=\frac{q}{2\mathrm{ϵ}}\left[N_A{\left(\frac{\mathrm{\delta }{N}^{\text{*}}}{N_A}\right)}^2+N_D{\left(\frac{\mathrm{\delta }{N}^{\text{*}}}{N_D}\right)}^2\right]$.