II.4 Recombinaison par centre piège

Lors de la définition du matériau extrinsèque, nous avions défini deux types de niveaux se situant dans la bande interdite; les niveaux de bord de bande qui interviennent dans le mécanisme de dopage et les niveaux profonds (situés vers le milieu de la bande interdite). Ces derniers ont un rôle fondamental dans les mécanismes de génération-recombinaison. Ils peuvent en effet servir de relais pour le passage des électrons et seront d'autant plus efficaces qu'ils se situent près du milieu de la bande interdite car les probabilités d'échanges avec les bandes de valence ou de conduction (émission ou capture d'électrons) seront alors sensiblement égales

Considérons le cas d'un semi-conducteur dans lequel existe un niveau piège. Ce dernier va pouvoir capturer puis réémettre des électrons après un certain temps correspondant au temps de piégeage.

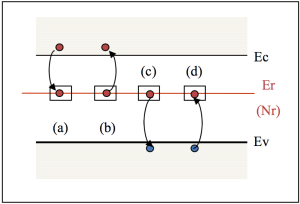
Les mécanismes d'échange entre les bandes et le niveau piège peuvent se modéliser par les quatre cas suivants :

(a) Capture d'un électron de la bande de conduction par un piège vide Cn

(b) Émission d'un électron vers la bande de conduction par un piège plein En

(c) Capture d'un trou de la bande de valence par un piège plein Cp

(d) Émission d'un trou dans la bande de valence par un piège vide Ep

Cn, En, Cp et Ep sont respectivement les coefficients de capture et d'émission des électrons et des trous.

Les centres pièges vont servir de « catalyseur » à la recombinaison des électrons libres en capturant ceux de la bande de conduction pour les réémettre vers la bande de valence (cas a puis c). On les appelle alors « centres de recombinaisons ».

Si le piège sert à piéger momentanément 1 trou (cas c puis d) ou 1 e- (ou cas a puis b) on l'appelle piège à trou ou à électron. Le temps pendant lequel le porteur reste « piégé » est plus ou moins long. C'est lui qui définit la durée de vie.

Il s'agit de modéliser les différents échanges afin d'en tirer une expression de la durée de vie des porteurs (Voir calcul [pdf]). Toutefois, ce calcul est simplement indicatif car il ne met en œuvre qu'un seul niveau piège ce qui ne reflète que partiellement la réalité. Les résultats obtenus sont malgré tout satisfaisants, l'écart par rapport aux mesures n'étant que de quelques pourcents.

Considérons le cas d'1 matériau dopé de type N ( n ¯ ≫ n ≫ p ¯ bar n >> n >> bar p ) en régime de faible injection n = n ¯ + n ^ ≈ n ¯ n = bar n+ hat n approx bar n

Fondamental

On trouve : r = n . p − n i 2 τ . ( n + p + 2 n i ) r= {n.p-n _{i} ^{2}} over {%tau .(n+p+2n _{i})} Formule de Shockley-Read

Considérons le cas d'1 matériau dopé de type N ( n ¯ ≫ n ≫ p ¯ bar n >> n >> bar p ) en régime de faible injection n = n ¯ + n ^ ≈ n ¯ n = bar n+ hat n approx bar n

On a alors r = n . p − n i 2 τ . n = p − n i 2 n τ = p − p ¯ τ = p ^ τ r = {n.p-n _{i} ^{2}} over {%tau .n} = {p-n _{i} ^{2} wideslash {n} } over {%tau } = { p-bar p} over {%tau} = hat p over %tau

La formule précédente est semblable à celle trouvée lors de la recombinaison directe électron-trou.

Fondamental

Les 2 taux de recombinaison sont additifs donc : r = p ^ τ r= hat p over %tau avec

1 τ = 1 τ recombinaisons directes + 1 τ recombinaisons par centre piège 1 over {%tau } = 1 over {%tau _{recombinaisons directes} } + { 1} over {%tau _{recombinaisons par centre piège}}