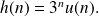3.3
Attention, votre navigateur ne supporte pas le javascript ou celui-ci a été désactivé. Certaines fonctionnalités dynamiques de ce module sont restreintes.
La fonction de transfert associée à cette équation de récurrence est (voir "question 1" ) :
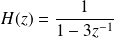
Méthode 1 :
D'après les pages 17 et 18 du cours, la réponse impulsionnelle est :
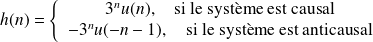
Le système étant causal :
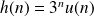
Méthode 2 :
La région de convergence d'un système causal est de la forme
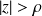, où
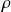est le maximum des modules des pôles de
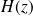. Pour
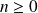, la fonction
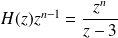est holomorphe sur
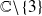. On peut donc lui appliquer le théorème des résidus sur un domaine délimité par un contour entourant l'origine et contenu dans le domaine de convergence. On obtient alors, d'après la formule d'inversion de la TZ
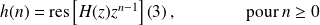
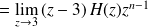
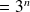
Puisque le système est causal, on a
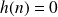pour
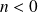. On retrouve donc le résultat
