Définitions fondamentales de l'ensemble canonique NVT : probabilité, fonction de partition et potentiel thermodynamique
Définition : Probabilité dans l'ensemble canonique NVT
distribution de Boltzmann : 
proportionnel à l'opposé de l'énergie Ei :
Il s'agit de la définition classique d'une probabilité :
où la distribution de Boltzmann représente la pondération de l'état i donc ZN représente tous les états du système, c-à-d la fonction de partition.
Les états les plus stables (de faible énergie) ont une probabilité plus grande.
corollaire : les états les plus stables contribuent plus à l'entropie S qui dépend de pi.
Définition : Fonction de partition de l'ensemble canonique NVT
On appelle fonction de partition la fonction qui décrit tous les états du système dans l'ensemble statistique considéré.
ZN est la fonction de partition de l'ensemble NVT. à l'aide de la contrainte 1 (somme des probabilités égale à 1), on déduit aisément :
cette expression va nous permettre plus loin dans le cours de dériver les équations d'états du gaz parfait et du viriel.
Définition : Potentiel thermodynamique de l'ensemble canonique NVT
On appelle potentiel thermodynamique = [ kB ] x [ ln fonction de partition ]
démonstration : pi introduit dans la formule de Gibbs donne :
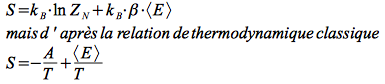
On déduit alors que le potentiel thermodynamique de l'ensemble canonique est la fonction -A/T :
où A est l'énergie libre (notée aussi F free energy dans les pays anglosaxons)Comme auparavant le potentiel thermodynamique est maximal dans l'état d'équilibre de l'ensemble ici NVT
Remarque : Relation entre les grandeurs microscopiques et macroscopiques
La formule est une illustration très importante de la thermodynamique statistique puisqu'elle relie la distribution microscopique (via la fonction de partition ZN décrivant tous les états microscopiques du système) aux grandeurs thermodynamiques macroscopiques.
Définition : Notion microscopique de la température
β est l'inverse de la température thermodynamique macroscopique. C'est la définition au sens de la mécanique statistique de la température :
Remarque : Définition de l'échelle des températures macroscopiques
La définition de β, prise comme une constante positive, implique que la grandeur T doit être forcément strictement positive. Elle définit alors l'échelle des températures selon Lord Kelvin qui est limitée par le zéro absolu, inatteignable.
