Particle filter
We have seen that the most general framework of nonlinear dynamics and non Gaussian distribution was build on the Bayes's rule.
Q: Is it possible to solve this dynamics directly?
A: Yes for linear dynamic and Gaussian distribution and the solution is provided by the Kalman's filter equations, but No in the general framework!!
While it is very simple, the Baye's rule is hard to achieve in practice, but a trick exists:
the particle filter
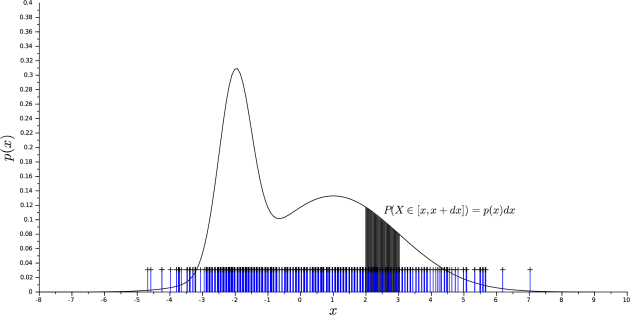
We know that when the number of sample is large, one can recover the distribution density from the emprirical density.
In terms of Dirac's distribution
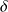the empirical density is
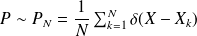
Analysis step
Thus, if one consider the empirical representation of the distribution
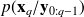as
then, the incorporation of information coming from new observations yq through the Baye's ruleis given by
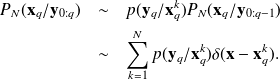
Hence, this takes the form
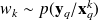with
.
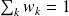If one assume that
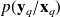is Gaussian with
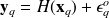, then
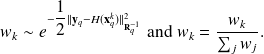
Resampling
There are many strategy for particle filter. Here, we chose a version where resampling occures at each step as follows.
From the weight wk that represent a discrete probability we sample
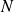new particles
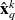where
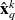is equal to
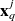with probability
.
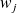We obtain after resampling, the following distribution
Forecast step
From this a posteriori distribution
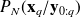, one can forecast the a priori
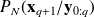thanks to the propagator (or flow associated to the dynamics)
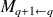as
Fundamental : Particle filter's algorithm
Starting with the prior discret distribution
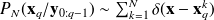
Analysis step:
Compute the weight
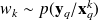,if Gaussian
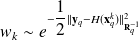.Resample
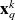where
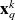is equal to
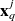with probability
.
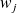Forecast step:
Compute the time evolution
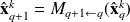,The new prior distribution is
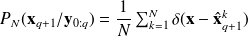
As an example, you can see the application of particle filter for:
Geophysical applications, see [vL09].
Fog forecasting, see [RPBB12].
Land surface model, see [ZME06].
...
Limitation for application of particle filter in large dimension system, see [SBBA08].
