Existence and unicity of solution
A very well known simple dynamical systems is provided by the linear oscillator whose equations are
This can be rewrited under the form
where
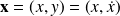And more generally, by introducing
we have
In the equation
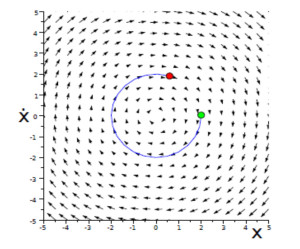
can be view as a field of vectors as shown on the following picture
 | And from a point, there exists one and only one trajectory
velocity of
the differential equation |
Phase space
The phase space denotes the space where
is living.
Q: Why is it interesting to consider this particular space?
A: Because interesting tools then exists!
For instance, the energy method:
Consider the quantity
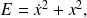
Its time derivative is given for the linear oscillator as
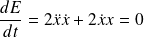
Can you explain what does it means?
This means that the energy introduced
is the distance between the origin of the phase-space
. The conservation
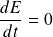
implies that the motion of the point is circular!
Note :
We have use new tools from geometry to tackle the bihaviour of the dynamics! This is what is new thanks to the phase-space representation.
Dynamical systems
A dynamical systems is defined by a dynamics
where there exists one and only one solution for each initial condition
of the phase space.
The existence and the unicity of solution is provided thanks to the Cauchy-Lipschitz theorem
Fundamental : Cauchy-Lipschitz theorem
We assume that the system
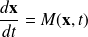is such that
is continuous and Lipshtzien in
that is
with
in an open set of
Then, there exists one and only one solution
of initial condition
.
The condition
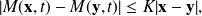is a regularity assumption that exclude singular vector fields.
Flow associated to a dynamical system
The flow associated to is the application
such that
is the only solution of initial state
.
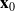