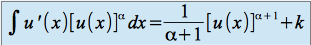Primitives et calcul intégral
Intégrale sur un segment
Fondamental : Propriété
Toute primitive d'une fonction 
continue sur 
s'écrit sous la forme
où 
est une constante réelle.
Si 
est une primitive de alors
Remarque :
Le résultat ne dépend pas de la primitive choisie.
En effet, si 
est une autre primitive de , on a : 
.
Et donc : 
Remarque :
Dans les calculs il est commode d'utiliser l'écriture :
Remarque :
Le choix de la variable d'intégration ne modifie pas le résultat : 
. On dit que la variable d'intégration est muette, on peut remplacer 
par n'importe quelle autre lettre (sauf les bornes 
ou 
).
Exemple :
Calculer 
et
On a :
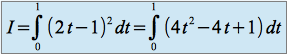
donc
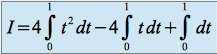
et donc
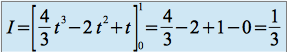
On a :
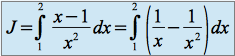
donc
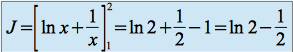
Intégrale indéfinie
Définition : Intégrale indéfinie
On désigne l'ensemble des primitives de par le symbole
qui se lit "somme de 
" et qui est appelée intégrale indéfinie.
Les propriétés de la dérivation de la composée de deux fonctions dérivables nous permettent de donner les propriétés suivantes :
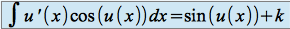
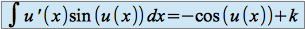
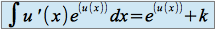
Si
ne s'annule pas, 
Si
ne s'annule pas lorsque 
et si est strictement positif lorsque 
n'est pas entier
Exemple
Exemple :
Déterminer
; 
et 
On a
donc
