Existence et unicité de IR
Nous admettrons l'existence et l'unicité d'un ensemble![]() , dont les éléments sont appelés les nombres réels, et qui est muni de deux lois internes
, dont les éléments sont appelés les nombres réels, et qui est muni de deux lois internes ![]() et
et ![]() , et d'une relation
, et d'une relation ![]() , tel que
, tel que
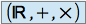 est un corps commutatif
est un corps commutatif est une relation d'ordre total dans
est une relation d'ordre total dans 
Toute partie non vide et majorée de
 admet une borne supérieure
admet une borne supérieure
Définition : Ensemble borné
Soit ![]() un sous ensemble de
un sous ensemble de ![]() . On dit que
. On dit que ![]() est borné si et seulement si
est borné si et seulement si ![]() est majorée et minorée
est majorée et minorée
Définition : Plus grand élément, plus petit élément
Soit ![]()
On dit que
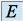 admet un plus grand élément
admet un plus grand élément
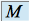 si et seulement si :
si et seulement si :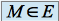 , et
, et 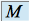 est un majorant de
est un majorant de 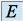
On note
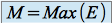
On dit que
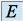 admet un plus petit élément
admet un plus petit élément
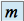 si et seulement si :
si et seulement si :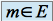 , et
, et 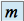 est un minorant de
est un minorant de 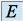
On note
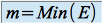
Définition : Borne supérieure, borne inférieure
soit![]()
On appelle borne supérieure le plus petit des majorants de
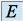 dans
dans  , s'il existe. On le note
, s'il existe. On le note 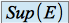
On appelle borne inférieure le plus grand des minorants de
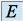 dans
dans  , s'il existe. On le note
, s'il existe. On le note 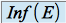
Définition : Intervalle de IR
Soient ![]() deux réels tels que
deux réels tels que ![]()
On appelle intervalle fermé de
 d'extrémité
d'extrémité  et
et  l'ensemble notée
l'ensemble notée 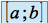 des
des 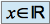 tels que
tels que 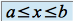 .
.On appelle intervalle ouvert de
 d'extrémité
d'extrémité  et
et  l'ensemble noté
l'ensemble noté 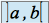 des
des  tels que
tels que 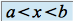 .
. On appelle intervalle fermé à gauche, ouvert à droite de
 d'extrémité
d'extrémité  et
et  l'ensemble noté
l'ensemble noté 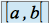 des
des  tels que
tels que 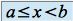 .
.On appelle intervalle ouvert à gauche, fermé à droite de
 d'extémité
d'extémité  et
et  l'ensemble noté
l'ensemble noté 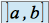 des
des  tels que
tels que 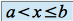 .
.On appelle intervalle semi-ouvert un intervalle fermé à gauche et ouvert à droite ou un intervalle ouvert à gauche et fermé à droite.
Définition : Voisinage d'un point
Soit
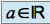 . On appelle voisinage de
. On appelle voisinage de  tout sous ensemble
tout sous ensemble 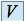 de
de  qui contient un intervalle ouvert contenant
qui contient un intervalle ouvert contenant  :
:Soit
 . On appelle voisinage de
. On appelle voisinage de  tout sous ensemble
tout sous ensemble 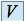 de
de  qui contient un sous ensemble du type
qui contient un sous ensemble du type  où
où  ,
,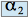 ,
, ,
,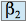 sont 4 réels strictement positifs.
sont 4 réels strictement positifs.Soit
 . On appelle voisinage de
. On appelle voisinage de  tout sous ensemble
tout sous ensemble 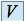 de
de  qui contient un sous ensemble du type
qui contient un sous ensemble du type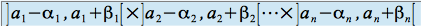 où
où 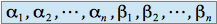 sont des réels strictement positifs.
sont des réels strictement positifs.
Remarque :
Dire que ![]() est un voisinage du point
est un voisinage du point ![]() signifie en fait que les points les "plus proches'' de
signifie en fait que les points les "plus proches'' de ![]() sont dans
sont dans ![]() .
.
Exemple :
Nous donnons ci-dessous deux exemples correspondant aux deux premiers cas de la définition
 est un voisinage de 2,1. Il suffit en effet de prendre
est un voisinage de 2,1. Il suffit en effet de prendre 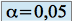 et
et 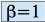 .
. n'est pas un voisinage de 5 car si
n'est pas un voisinage de 5 car si  nous avons toujours
nous avons toujours  .
.L'ensemble
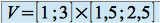 représenté ci-dessous est un voisinage du point
représenté ci-dessous est un voisinage du point 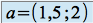 .
.





