Fonctions réciproques des fonctions hyperboliques et leurs dérivées
Fonction argument sinus hyperbolique
La fonction sh est continue et strictement croissante sur 
, elle réalise une bijection de sur Elle admet donc une fonction réciproque notée argsh, définie de la façon suivante :
Après calcul, on obtient une expression logarithmique de cette fonction, sous la forme :
Cette fonction est dérivable sur et on obtient :
Fonction argument cosinus hyperbolique
De même la fonction ch est continue et strictement croissante sur 
, elle réalise une bijection de sur 
. Elle admet donc une fonction réciproque notée argch, définie de la façon suivante :
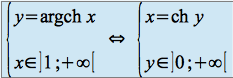
Après calcul, on obtient une expression logarithmique de cette fonction, sous la forme :
Cette fonction est dérivable sur son domaine de définition et on obtient :
Fonction argument tangente hyperbolique
De même la fonction th est continue et strictement croissante sur , elle réalise une bijection de sur 
. Elle admet donc une fonction réciproque notée argth, définie de la façon suivante :
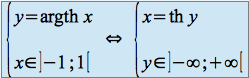
Après calcul, on obtient une expression logarithmique de cette fonction, sous la forme :
Cette fonction est dérivable sur son domaine de définition et on obtient :
