Fonctions réciproques des fonctions trigonométriques et leurs dérivées
Fonction arcsinus
La fonction sin est continue et strictement croissante sur 
, elle réalise une bijection de sur 
. Elle admet donc une fonction réciproque notée arcsin, définie de la façon suivante :
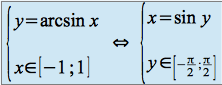
Sa dérivée se calcule en utilisant la formule de dérivation de la fonction réciproque d'une fonction bijective :
On obtient :
avec 
et 
Or
avec 
Finalement, la fonction arcsin est dérivable sur 
et
Fonction arccosinus
La fonction cos est continue et strictement décroissante sur 
, elle réalise une bijection de sur . Elle admet donc une fonction réciproque notée arccos, définie de la façon suivante :
La fonction arccos est dérivable sur et
Fonction arctangente
La fonction tan est continue et strictement croissante sur , elle réalise une bijection de sur 
. Elle admet donc une fonction réciproque notée arctan, définie de la façon suivante :
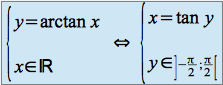
La fonction arctan est dérivable sur et
