Vecteurs propres et valeurs propres - Espaces propres
Définition : Vecteurs propres et valeurs propres
Soit 
un 
-espace vectoriel de dimension finie, et soit 
un endomorphisme de . Un vecteur 
est appelé vecteur propre de si et seulement si : 
est non nul, et il existe un scalaire 
tel que 
.
Le scalaire 
est alors appelé valeur propre de associée au vecteur propre .
Remarque :
Tout vecteur non nul colinéaire à un vecteur propre est aussi vecteur propre.
Si l'endomorphisme
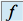n'est pas injectif, alors il admet un noyau et tout vecteur non nul dans 
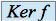est un vecteur propre associé à la valeur propre 0.Par contre, le vecteur nul n'est jamais un vecteur propre !
Définition :
On appelle spectre d'un endomorphisme , l'ensemble des valeurs propres de .
Définition : Espaces propres
Soit un -espace vectoriel de dimension finie et un endomorphisme de . Soit une valeur propre de l'endomorphisme . On appelle espace propre de associé à , l'ensemble
Cas particulier : on appelle direction propre tout sous espace vectoriel de dimension 1 engendré par un seul vecteur propre.
Fondamental : Propriété
Soit un -espace vectoriel de dimension finie et un endomorphisme de . Tout espace propre de est un sous-espace vectoriel de .
La particularité de ces sous-espaces vectoriels est d'être invariants par transformation avec l'endomorphisme , c'est à dire que
Ceci est aussi vrai pour toute direction propre, qui est effectivement "conservée'' par transformation avec , et par conséquent, tout sous-espace vectoriel d'un espace propre 
de l'endomorphisme est aussi invariant par .
Fondamental : Théorème
Soit un -espace vectoriel de dimension finie et un endomorphisme de . Si 
(scalaires dans le corps ), sont 
valeurs propres distinctes de , alors les espaces propres associés 
, sont en somme directe dans , c'est à dire que l'union des bases de chacun de ces espaces propres forme une famille libre dans (mais attention, pas forcément génératrice dans ).
