Définition du produit matriciel
Définition :
Pour multiplier deux matrices, on utilise le produit ligne par colonne introduit précédemment.
Pour que ce produit soit possible, il faut que le nombre de colonnes de la première matrice soit égal au nombre de ligne de la deuxième, à savoir :
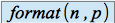multiplié par 
.
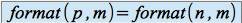De manière plus précise, la multiplication de deux matrices,
dans 
et
dans 
, notée 
, est définie par :
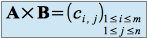, avec 
,
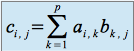le résultat étant dans 
.
Remarque :
Le signe de multiplication entre matrices "x" est en règle générale omis (pour simplifier), et on écrit la produit de
par
:
Fondamental : Propriété
Dans le cas de la multiplication de plusieurs matrices, le produit matriciel est une opération associative, et on a donc, le cas du produit de trois matrices par exemple :
ATTENTION : Le produit matriciel n'est pas commutatif (ne serait-ce que pour de simples raisons de compatibilité entre le nombre de colonnes et nombre de lignes entre les matrices de ce produit) !
Le produit matriciel est une opération distributive par rapport à l'addition des matrices.
Exemple :
format (2,3) multiplié par format (3,2) = format (2,2)
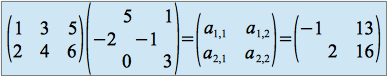
chacun des termes a i,j du résultat étant égal au produit de la ligne
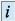de la première matrice par la colonne 
de la deuxième matrice.Par exemple,
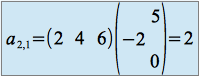
format (3,4) multiplié par format (4,2) = format (3,2)
.
