Généralisation
Introduction
Si 
est une application linéaire d'un espace vectoriel 
de dimension 
vers un espace vectoriel 
de dimension 
, est entièrement définie par l'image des vecteurs d'une base de .
Ces images étant dans , elles peuvent s'exprimer de façon unique dans une base de donnée.
Fixons donc une base 
de et 
une base de .
Du fait de la linéarité de , les coordonnées des vecteurs 
dans la base
définissent parfaitement . Ces coordonnées définissent un tableau ayant colonnes : les coordonnées des vecteurs , et de lignes (chacun de ces vecteurs ayant coordonnées dans la base . Ce tableau est appelé matrice de et dépend des bases choisies dans et . On écrira :
ou encore 
.
Exemple :
Soit l'application linéaire de 
, de base canonique 
, dans 
, de base canonique 
, et définie par :
, avec 
,
On calcule : 
,
,
dans la base canonique de .
DANS LES BASES CANONIQUES, 
, 
, 
, et a pour matrice :
Ainsi 
(ou de manière équivalente, 
) est l'ensemble des vecteurs 
de tels que 
, c'est à dire, matriciellement parlant, tels que :
C'est l'ensemble des vecteurs
de suivants :
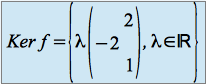
C'est un sous-espace vectoriel dede dimension 1.
On peut vérifier, en outre, que
tout entier, parce que
ensemble de trois vecteurs de dans lequel les deux premiers, par exemple, sont trivialement libres...
