Matrice d'une application linéaire
Matrice d'une application linéaire
Dans la base canonique 
de 
, on définit l'application linéaire 
de dans par :
.
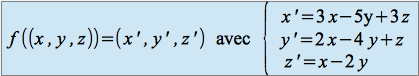Question
Ecrire la matrice 
de dans la base canonique de .
On obtient naturellement :
.
Question
On définit :
.
Montrer que
est une base de .Déterminer la matrice
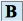de 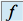dans la base .
L'espace vectoriel
étant de dimension 3, est une base de si et seulement si c'est une famille libre. A cet égard, on a :
,
ce qui, puisque est une famille libre de , impose que :
,
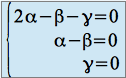c'est à dire : 
. Ainsi :
et la famille est donc libre. C'est une base de .
Calculons les coordonnées de
, 
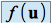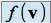, et 
, dans la base .Les coordonnées de
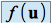dans la base canonique 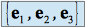sont données par :
,
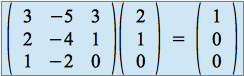d'où 
.
Les coordonnées de dans la base canonique sont données par :
,
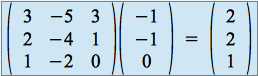d'où 
.
Les coordonnées de dans la base canonique sont données par :
,
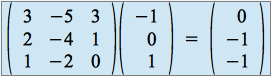d'où 
.
Enfin, à partir du système
,
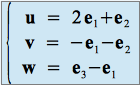on exprime en fonction de . On obtient :
,
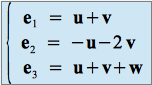et finalement on a :
, 
et 
.
La matrice de dans la base est donc :
.
